Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông cân tại \(B\), cạnh bên \(SA\) vuông góc với mặt phẳng đáy, \(AB = BC = a\) và \(SA = a\). Góc giữa hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBC} \right)\) bằng
Trả lời bởi giáo viên
Đáp án đúng: a
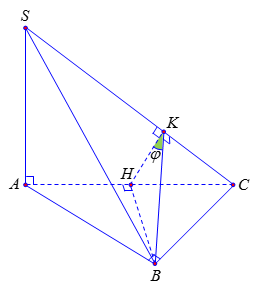
Gọi \(H\) là trung điểm cạnh \(AC\)
Ta có \(\left( {SAC} \right) \bot \left( {ABC} \right)\) (vì \(SA \bot \left( {ABC} \right)\)) và \(BH \bot AC\)\( \Rightarrow BH \bot \left( {SAC} \right)\).
Trong mặt phẳng \(\left( {SAC} \right)\), kẻ \(HK \bot SC\) thì \(SC \bot \left( {BHK} \right)\)\( \Rightarrow SC \bot BK\).
\( \Rightarrow \left( {\widehat {\left( {SAC} \right),\,\left( {SBC} \right)}} \right) = \widehat {SKH} = \varphi \).
Mặt khác
Tam giác \(ABC\) vuông cân tại \(B\) có \(AB = BC = a\) nên \(AC = a\sqrt 2 \) và \(BH = \dfrac{{a\sqrt 2 }}{2}\).
Hai tam giác \(CKH\) và $CAS$ đồng dạng nên \(HK = \dfrac{{HC.SA}}{{SC}}\) \( \Leftrightarrow HK = \dfrac{{HC.SA}}{{\sqrt {S{A^2} + A{C^2}} }} = \dfrac{{a\sqrt 2 }}{{\sqrt 3 }}\).
Tam giác \(BHK\) vuông tại \(H\) có \(\tan \varphi = \dfrac{{BH}}{{BK}} = \sqrt 3 \) \( \Rightarrow \varphi = 60^\circ \).
Vậy \(\left( {\widehat {\left( {SAC} \right),\,\left( {SBC} \right)}} \right) = 60^\circ \).
Hướng dẫn giải:
Xác định góc giữa hai mặt phẳng: là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
