Câu hỏi:
2 năm trước
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi tâm $O$, đường thẳng $SO$ vuông góc với mặt phẳng $\left( {ABCD} \right)$. Biết \(BC = SB = a,SO = \dfrac{{a\sqrt 6 }}{3}\). Tìm số đo của góc giữa hai mặt phẳng $\left( {SBC} \right)$và $\left( {SCD} \right)$.
Trả lời bởi giáo viên
Đáp án đúng: a
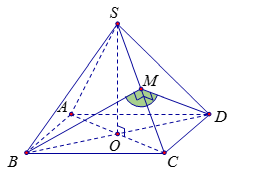
Gọi \(M\) là trung điểm của \(SC\), do tam giác \(SBC\) cân tại \(B\) nên ta có \(SC \bot BM\) (1).
Theo giả thiết ta có \(BD \bot \left( {SAC} \right) \Rightarrow SC \bot BD\). Do đó $SC \bot \left( {BCM} \right)$ suy ra $SC \bot DM$ (2).
Từ (1) và (2) suy ra góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SCD} \right)\) là góc giữa hai đường thẳng \(BM\) và $DM$.
Ta có \(\Delta SBO = \Delta CBO\) suy ra \(SO = CO = \dfrac{{a\sqrt 6 }}{3}\).
Do đó \(OM = \dfrac{1}{2}SC = \dfrac{{a\sqrt 3 }}{3}\).
Mặt khác \(OB = \sqrt {S{B^2} - S{O^2}} = \dfrac{{a\sqrt 3 }}{3}\). Do đó tam giác \(BMO\) vuông cân tại \(M\) hay góc \(\widehat {BMO} = 45^\circ \), suy ra \(\widehat {BMD} = 90^\circ \).
Vậy góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {SCD} \right)\) là \(90^\circ \).
Hướng dẫn giải:
- Xác định giao tuyến của hai mặt phẳng.
- Dựng các đường thẳng lần lượt vuông góc với giao tuyến mà nằm trong hai mặt phẳng.
- Góc giữa hai mặt phẳng bằng góc giữa hai giao tuyến trên.
- Tính góc dựa vào các kiến thức hình học đã biết.
