Câu hỏi:
2 năm trước
Cho hình chóp \(S.ABC\) có cạnh \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\), biết \(AB = AC = a\), \(BC = a\sqrt 3 \). Tính góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\).
Trả lời bởi giáo viên
Đáp án đúng: c
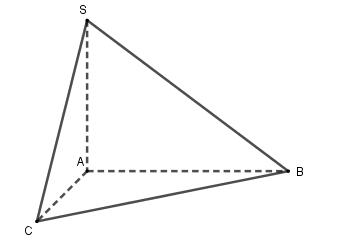
Vì \(SA \bot \left( {ABC} \right)\) nên \(SA \bot AB\) và \(SA \bot AC\).
ta có: $\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {SAC} \right) = SA\\SA \bot AB\\SA \bot AC\end{array} \right.$ $ \Rightarrow \left( {\widehat {\left( {SAB} \right),\left( {SAC} \right)}} \right) = \left( {\widehat {AB,AC}} \right)$.
Xét $\Delta ABC$ có $\cos \widehat {BAC} = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}}$ $ = \dfrac{{{a^2} + {a^2} - {{\left( {a\sqrt 3 } \right)}^2}}}{{2.a.a}} = - \dfrac{1}{2}$ $ \Rightarrow \widehat {BAC} = 120^\circ $.
Do đó $\left( {\widehat {AB,AC}} \right) = {180^0} - {120^0} = {60^0}$ (vì góc giữa hai đường thẳng không thể lớn hơn \({90^0}\)).
Vậy góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) là \({60^0}\).
Hướng dẫn giải:
Xác định góc giữa hai mặt phẳng: là góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng mà cùng vuông góc với giao tuyến.
