Câu hỏi:
2 năm trước
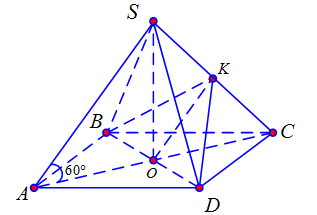
Cho hình chóp đều $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a\sqrt 2 $, biết các cạnh bên tạo với đáy một góc $60^\circ $. Giá trị lượng giác tang của góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SCD} \right)$ bằng
Trả lời bởi giáo viên
Đáp án đúng: a
Kẻ $OK \bot SC$. Do $S.ABCD$ là hình chóp đều và $ABCD$ là hình vuông nên $SO \bot \left( {ABCD} \right)$; $BD \bot \left( {SAC} \right) \Rightarrow SC \bot BD$. Suy ra $SC \bot \left( {BKD} \right) \Rightarrow KD \bot SC$.
Vậy góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SCD} \right)$ là $\widehat {OKD}$ và $\tan \widehat {OKD} = \dfrac{{OD}}{{OK}}$ (do $\Delta KOD$ vuông ở $O$): $ABCD$ là hình vuông cạnh $a\sqrt 2 $ nên $AC = 2a \Rightarrow OA = OC = OD = a$.
Trong hình chóp đều $S.ABCD$, cạnh bên tạo với đáy một góc $60^\circ $ nên $\widehat {SAC} = 60^\circ $
$ \Rightarrow SO = OA.\tan 60^\circ = a\sqrt 3 $.
Ta có $\dfrac{1}{{O{K^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{C^2}}} \Rightarrow OK = \dfrac{{a\sqrt 3 }}{2}$$ \Rightarrow \tan \widehat {OKD} = \dfrac{{OD}}{{OK}} = \dfrac{2}{{\sqrt 3 }} = \dfrac{{2\sqrt 3 }}{3}$.
