Câu hỏi:
2 năm trước
Cho hình chóp $S .A B C D$ có đáy là hình chữ nhật, \(AB = 2a,AD = a;\) tam giác $S A B$ đều và nằm trong mặt phẳng vuông góc với đáy. Góc \(\alpha \) tạo bởi hai mặt phẳng \((SCD)\) và \((ABCD)\) có số đo bằng
Trả lời bởi giáo viên
Đáp án đúng: c
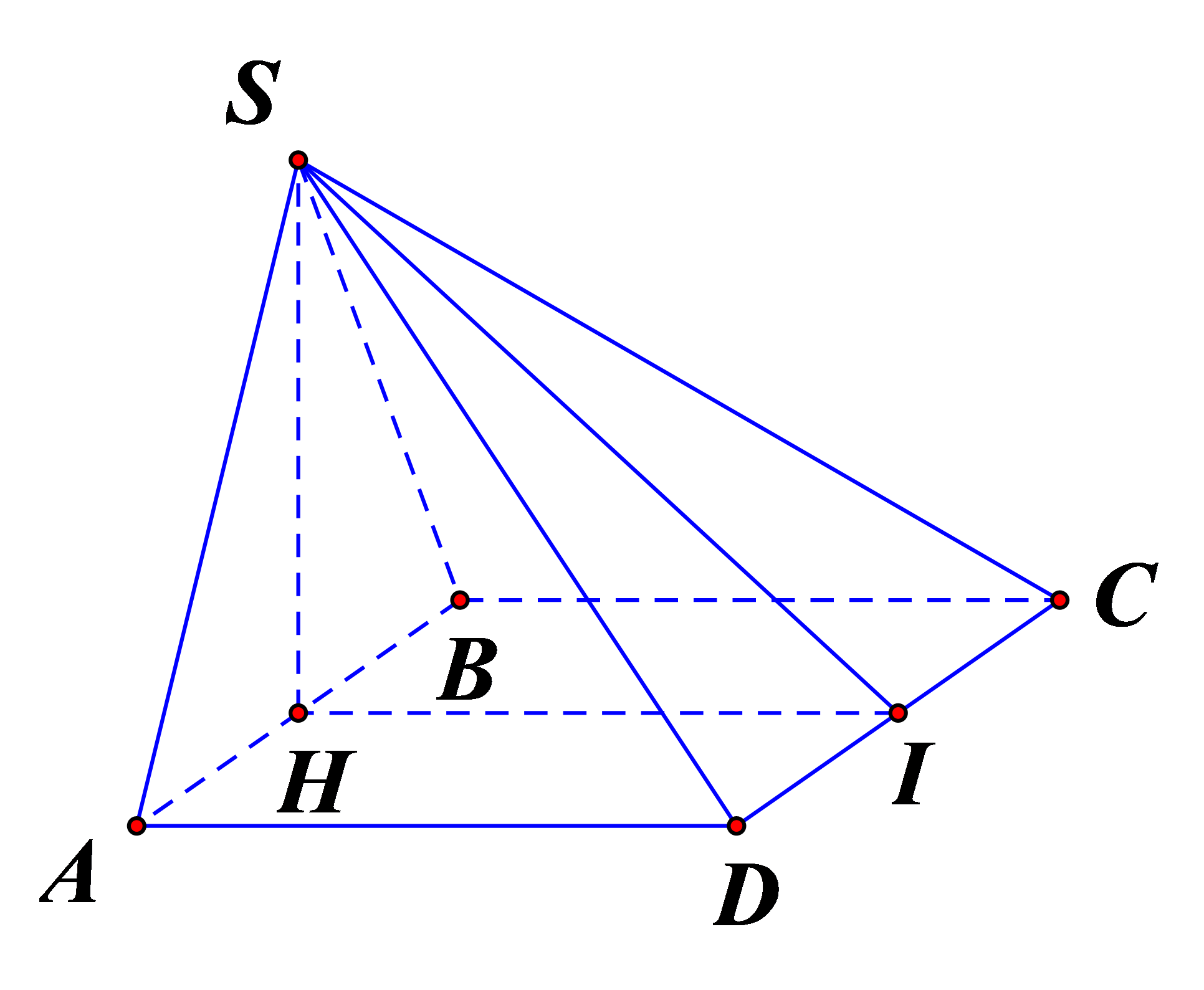
Gọi \(H\) là trung điểm $A B$, do tam giác $S A B$ đều nên \(SH \bot AB\). Mà \((SAB) \bot (ABCD)\) nên \(SH \bot (ABCD)\).
Gọi \(I\) là trung điểm $C D$.
Ta có: \(\alpha = ((SCD);(ABCD)) = \widehat {SIH}\).
Trong đó: $S H$ là đường cao của tam giác đều cạnh 2a nên \(SH = a\sqrt 3 ,HI = AD = a\).
Khi đó \(\tan \alpha = \tan \widehat {SIH} = \dfrac{{SH}}{{HI}} = \sqrt 3 \), suy ra \(\alpha = {60^0 }\).
Hướng dẫn giải:
Bước 1: Gọi \(H\) là trung điểm $A B$. Chứng minh \(SH \bot (ABCD)\).
Bước 2: Gọi \(I\) là trung điểm $C D$. Tính \(((SCD);(ABCD))\)
