Câu hỏi:
2 năm trước
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $2a$. Gọi $O$ là giao điểm của $AC$ và $BD$. Biết hình chiếu vuông góc của đỉnh $S$ trên mặt phẳng $\left( {ABCD} \right)$ là trung điểm $H$ của đoạn $OA$ và góc $\widehat {\left( {SD;\left( {ABCD} \right)} \right)} = 60^\circ $. Gọi $\alpha $ là góc giữa hai mặt phẳng $\left( {SCD} \right)$ và $\left( {ABCD} \right)$. Tính $\tan \alpha $.
Trả lời bởi giáo viên
Đáp án đúng: d
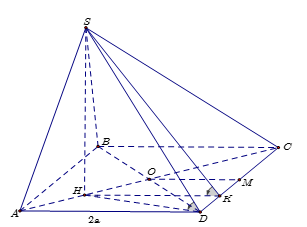
Ta có $SH \bot \left( {ABCD} \right)$ suy ra góc giữa $SD$ và mặt phẳng $\left( {ABCD} \right)$ chính là góc $\widehat {SDH}$ hay $\widehat {SDH} = 60^\circ $.
Hạ $HK \bot CD$ suy ra $CD \bot \left( {SHK} \right)$ nên góc giữa hai mặt phẳng $\left( {SCD} \right)$ và $\left( {ABCD} \right)$ là góc $\widehat {SKH}$ suy ra $\widehat {SKH} = \alpha $.
Ta có $DH = \sqrt {O{H^2} + O{D^2}} = \sqrt {{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} = \dfrac{{a\sqrt 5 }}{{\sqrt 2 }}$.
Tam giác $SHD$ là nửa tam giác đều cạnh $SD = 2DH = a\sqrt {10} $ suy ra đường cao $SH = \dfrac{{\left( {a\sqrt {10} } \right)\sqrt 3 }}{2} = \dfrac{{a\sqrt {30} }}{2}$.
Gọi $M$ là trung điểm $CD$, ta có $HK = \dfrac{{OM + AD}}{2} = \dfrac{{3a}}{2}$.
Vậy $\tan \alpha = \dfrac{{SH}}{{HK}} = \dfrac{{\dfrac{{a\sqrt {30} }}{2}}}{{\dfrac{{3a}}{2}}} = \dfrac{{\sqrt {30} }}{3}$.
Hướng dẫn giải:
- Xác định giao tuyến của hai mặt phẳng.
- Xác định các đường thẳng lần lượt thuộc hai mặt phẳng mà vuông góc với giao tuyến.
- Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng trên.
- Tính toán dựa vào các kiến thức đã biết ở lớp dưới.
