HĐ2
Cho hai vectơ cùng phương →u=(x;y) và →v=(kx;ky). Hãy kiểm tra công thức →u.→v=k(x2+y2) theo từng trường hợp sau:
a) →u=→0
b) →u≠→0 và k≥0
c) →u≠→0 và k<0
Phương pháp giải:
Tính tích vô hướng bằng công thức: →u.→v=|→u|.|→v|.cos(→u,→v)
Lời giải chi tiết:
a) Vì →u=→0 nên →u vuông góc với mọi →v.
Như vậy →u.→v=0
Mặt khác: →u=→0⇔x=y=0
⇒k(x2+y2)=0=→u.→v
b) Vì →u≠→0 và k≥0 nên →u và →vcùng hướng.
⇒(→u,→v)=0o⇔cos(→u,→v)=1
⇒→u.→v=|→u|.|→v|=√x2+y2.√(kx)2+(ky)2=√x2+y2.|k|.√x2+y2=k(x2+y2)
(|k|= k do k > 0)
c) Vì →u≠→0 và k<0 nên →u và →vngược hướng.
⇒(→u,→v)=180o⇔cos(→u,→v)=−1
⇒→u.→v=−|→u|.|→v|=−√x2+y2.√(kx)2+(ky)2=−√x2+y2.|k|.√x2+y2=k(x2+y2).
HĐ3
Trong mặt phẳng tọa độ Oxy, cho hai vectơ không cùng phương →u=(x;y) và →v=(x′;y′).
a) Xác định tọa độ của các điểm A và B sao cho →OA=→u,→OB=→v.
b) Tính AB2,OA2,OB2 theo tọa độ của A và B.
c) Tính →OA.→OB theo tọa độ của A, B.
Lời giải chi tiết:
a) Vì →OA=→u=(x;y) nên A(x; y).
Tương tự: do →OB=→v=(x′;y′) nên B (x’; y’)
b) Ta có: →OA=(x;y)⇒OA2=|→OA|2=x2+y2.
Và →OB=(x′;y′)⇒OB2=|→OB|2=x′2+y′2.
Lại có: →AB=→OB−→OA=(x′;y′)−(x;y)=(x′−x;y′−y)
⇒AB2=|→AB|2=(x′−x)2+(y′−y)2.
c) Theo định lí cosin trong tam giác OAB ta có:
cosˆO=OA2+OB2−AB22.OA.OB
Mà →OA.→OB=|→OA|.|→OB|.cos(→OA,→OB)=OA.OB.cosˆO
⇒→OA.→OB=OA.OB.OA2+OB2−AB22.OA.OB=OA2+OB2−AB22
⇒→OA.→OB=x2+y2+x′2+y′2−(x′−x)2−(y′−y)22⇔→OA.→OB=−(−2x′.x)−(−2y′.y)2=x′.x+y′.y
Luyện tập 3
Tích vô hướng và góc giữa hai vectơ →u=(0;−5),→v=(√3;1)
Phương pháp giải:
Cho →u=(x;y) và →v=(x′;y′), khi đó: →u.→v=x.x′+y.y′
Lời giải chi tiết:
Ta có: →u=(0;−5),→v=(√3;1)
⇒→u.→v=0.√3+(−5).1=−5.
HĐ4
Cho ba vectơ →u=(x1;y1),→v=(x2;y2),→w=(x3;y3).
a) Tính →u.(→v+→w),→u.→v+→u.→w theo tọa độ của các vectơ →u,→v,→w.
b) So sánh →u.(→v+→w) và →u.→v+→u.→w
c) So sánh →u.→v và →v.→u
Phương pháp giải:
Cho →u=(x;y) và →v=(x′;y′), khi đó: →u.→v=x.x′+y.y′
Lời giải chi tiết:
a) Ta có: →u=(x1;y1),→v=(x2;y2),→w=(x3;y3).
⇒→v+→w=(x2;y2)+(x3;y3)=(x2+x3;y2+y3)⇒→u.(→v+→w)=x1.(x2+x3)+y1.(y2+y3)
Và: →u.→v+→u.→w=(x1.x2+y1.y2)+(x1.x3+y1.y3)=x1.x2+y1.y2+x1.x3+y1.y3.
b) Vì x1.x2+y1.y2+x1.x3+y1.y3=(x1.x2+x1.x3)+(y1.y2+y1.y3)=x1.(x2+x3)+y1.(y2+y3)
Nên →u.(→v+→w)=→u.→v+→u.→w
c) Ta có: →u=(x1;y1),→v=(x2;y2)
⇒{→u.→v=x1.x2+y1.y2→v.→u=x2.x1+y2.y1⇔→u.→v=→v.→u
Luyện tập 4
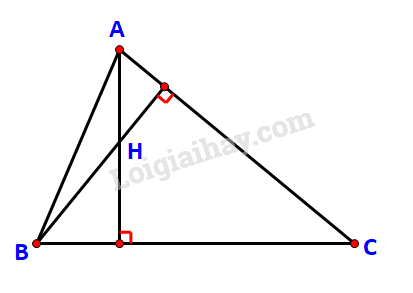
Cho tam giác ABC với A(-1; 2), B(8; -1), C(8; 8). Gọi H là trực tâm của tam giác.
a) Chứng minh rằng →AH.→BC=→0 và →BH.→CA=→0
b) Tìm tọa độ của H.
c) Giải tam giác ABC.
Phương pháp giải:
a) →u⊥→v⇔→u.→v=0
b) Lập hệ PT biết →AH.→BC=→0 và →BH.→CA=→0.
c) Nếu vectơ →AB(x;y) thì |→AB|=√x2+y2
Lời giải chi tiết:
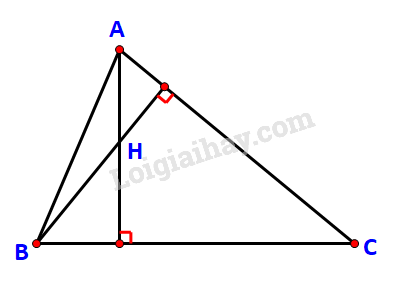
a) AH⊥BC và BH⊥CA
⇒(→AH,→BC)=90o⇔cos(→AH,→BC)=0 . Do đó →AH.→BC=→0
Tương tự suy ra →BH.→CA=→0.
b) Gọi H có tọa độ (x; y)
⇒{→AH=(x−(−1);y−2)=(x+1;y−2)→BH=(x−8;y−(−1))=(x−8;y+1)
Ta có: →AH.→BC=→0 và →BC=(8−8;8−(−1))=(0;9)
(x+1).0+(y−2).9=0⇔9.(y−2)=0⇔y=2.
Lại có: →BH.→CA=→0 và →CA=(−1−8;2−8)=(−9;−6)
(x−8).(−9)+(y+1).(−6)=0⇔−9x+72+3.(−6)=0⇔−9x+54=0⇔x=6.
Vậy H có tọa độ (6; 2)
c) Ta có: →AB=(8−(−1);−1−2)=(9;−3)⇒AB=|→AB|=√92+(−3)2=3√10
Và →BC=(0;9)⇒BC=|→BC|=√02+92=9;
→CA=(−9;−6)⇒AC=|→CA|=√(−9)2+(−6)2=3√13.
Áp dụng định lí cosin cho tam giác ABC, ta có:
cosˆA=b2+c2−a22bc=(3√13)2+(3√10)2−(9)22.3√13.3√10≈0,614⇒ˆA≈52,125o
cosˆB=a2+c2−b22ac=(9)2+(3√10)2−(3√13)22.9.3√10=√1010⇒ˆB≈71,565o
⇒ˆC≈56,31o
Vậy tam giác ABC có: a=9;b=3√13;c=3√10; ˆA≈52,125o;ˆB≈71,565o;ˆC≈56,31o.
Vận dụng
Một lực →F không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng từ A đến B. Lực →F được phân tích thành hai lực thành phần là →F1 và →F2 (→F=→F1+→F2).
a) Dựa vào tính chất của tích vô hướng, hãy giải thích vì sao công sinh bởi lực →F (đã được đề cập ở trên) bằng tổng của các công sinh bởi các lực →F1 và →F2.
b) Giả sử các lực thành phần →F1, →F2tương ứng cùng phương, vuông góc với phương chuyển động của vật. Hãy tìm mối quan hệ giữa các công sinh bởi lực →F và lực →F1.
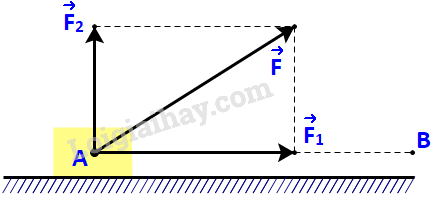
Phương pháp giải:
Khi lực →F không đổi tác dụng lên một vật và điểm đặt chuyển dời một đoạn s theo hướng hợp với hướng của lực góc α thì công sinh bởi lực đó là: A=F.s.cosα
Lời giải chi tiết:
a)

Gọi A,A1,A2 lần lượt là công sinh bởi lực →F, →F1 và →F2.
Ta cần chứng minh: A=A1+A2
Xét lực →F, công sinh bởi lực →F là: A=|→F|.AB.cos(→F,→AB)=→F.→AB
Tương tự, ta có: A1=→F1.→AB, A2=→F2.→AB
Áp dụng tính chất của tích vô hướng ta có:
A1+A2=→F1.→AB+→F2.→AB=(→F1+→F2).→AB=→F.→AB=A
b)
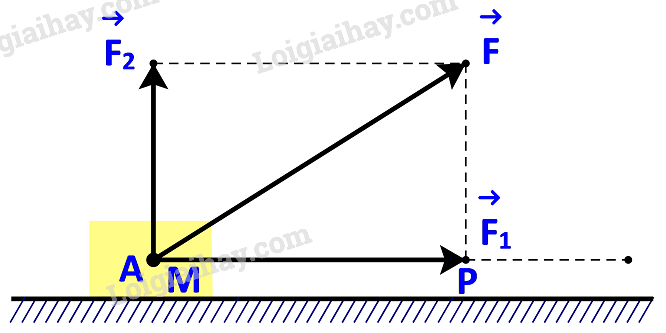
Vì →F2tương ứng vuông góc với phương chuyển động nên →F2⊥→AB
Do đó: công sinh bởi lực →F2 là: A2=→F2.→AB=0
Mà A=A1+A2
⇒A=A1
Vậy công sinh bởi lực →F bằng công sinh bởi lực →F1.

