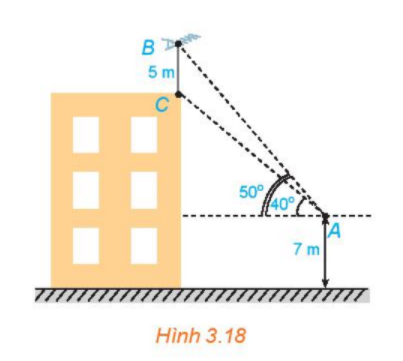
Trên nóc một tòa nhà có một cột ăng-ten cao 5m. Từ một vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng-ten, với các góc tương ứng là 50ovà 40o so với phương nằm ngang (H.3.18).
a) Tính các góc của tam giác ABC.
b) Tính chiều cao của tòa nhà.
LG a
a) Tính các góc của tam giác ABC.
Phương pháp giải:
Nhắc lại: Tổng ba góc của một tam giác luôn bằng 180o.
Bước 1: Gọi H là hình chiếu của A lên đường thẳng BC.
Bước 2: Tính góc ^BAC, góc ^ABC => góc ^BCA.
Lời giải chi tiết:
Gọi H là hình chiếu của A lên đường thẳng BC.
Ta có: ^HAB=50o; ^HAC=40o
⇒^BAC=50o−40o=10o (1)
Xét tam giác ABH, vuông tại H ta có:
ˆH=90o;^BAH=50o.
⇒^HBA=180o−90o−50o=40o hay ^CBA=40o. (2)
Từ (1) và (2), suy ra: ^BCA=180o−40o−10o=130o.
Vậy ba góc của tam giác ABC lần lượt là: ˆA=10o;ˆB=40o;ˆC=130o.
LG b
b) Tính chiều cao của tòa nhà.
Phương pháp giải:
Bước 1: Tính AB: AB=BC.sinCsinA
Bước 2: Tính BH => chiều cao của tòa nhà = BH + độ cao của vị trí quan sát.
Lời giải chi tiết:
Áp dụng định lý sin cho tam giác ABC, ta được:
BCsinA=ACsinB=ABsinC ⇒AB=BC.sinCsinA
Mà: BC=5(m);ˆC=130o;ˆA=10o
⇒AB=5.sin130osin10o≈22(m)
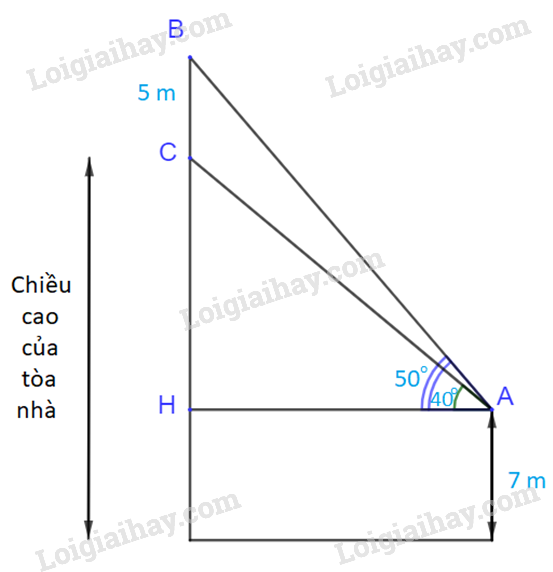
Xét tam giác ABH, vuông tại H ta có:
sin^BAH=BHAB⇒BH=AB.sin^BAH
Mà: AB≈22(m);^BAH=50o
⇒BH≈22.sin50o≈16,85(m)
Vậy chiều cao của tòa nhà là: BH−BC+7=16,85−5+7=18,85(m)
