HĐ1
Cho vecto \(\overrightarrow {AB} = \overrightarrow a \). Hãy xác định điểm C sao cho \(\overrightarrow {BC} = \overrightarrow a \)
a) Tìm mối quan hệ giữa \(\overrightarrow {AB} \) và \(\overrightarrow a + \overrightarrow a \)
b) Vecto \(\overrightarrow a + \overrightarrow a \) có mối quan hệ như thế nào về hướng và độ dài đối với vecto \(\overrightarrow a \)
Phương pháp giải:
Hai vecto bằng nhau nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
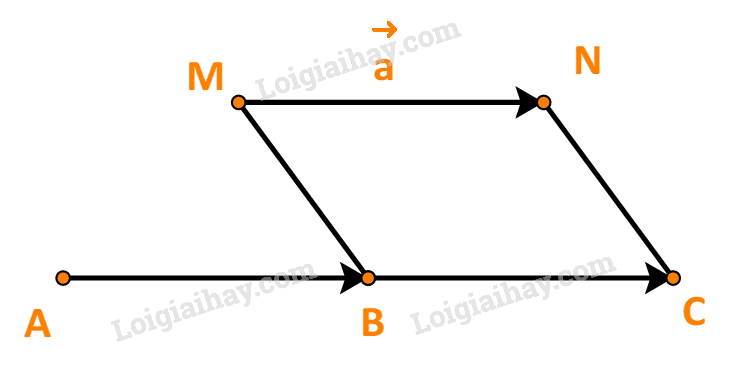
Gọi M, N lần lượt là điểm đầu và điểm cuối của vecto \(\overrightarrow a \).
Từ B, M, N ta dựng hình bình hành BMNC.
Khi đó: \(\overrightarrow {MN} = \overrightarrow {BC} \) hay \(\overrightarrow a = \overrightarrow {BC} \).
\( \Rightarrow \overrightarrow a + \overrightarrow a = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
a) Vì \(\overrightarrow {AB} = \overrightarrow a = \overrightarrow {BC} \) nên A, B, C thẳng hàng và B là trung điểm của AC.
Vậy \(\overrightarrow a + \overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng, \(\left| {\overrightarrow a + \overrightarrow a } \right| = 2.\left| {\overrightarrow {AB} } \right|\)
b) Ta có: \(\overrightarrow a + \overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng, \(\left| {\overrightarrow a + \overrightarrow a } \right| = 2.\left| {\overrightarrow {AB} } \right|\)
Mà \(\overrightarrow {AB} = \overrightarrow a \) nên: \(\overrightarrow a + \overrightarrow a \) và \(\overrightarrow a \) cùng hướng, \(\left| {\overrightarrow a + \overrightarrow a } \right| = 2.\left| {\overrightarrow a } \right|\).
Câu hỏi
\(1\;\overrightarrow a \) và \(\overrightarrow a \) có bằng nhau hay không?
Phương pháp giải:
Hai vecto bằng nhau nếu chúng có cùng độ dài và cùng hướng.
Lời giải chi tiết:
Ta có: Vecto \(1\;\overrightarrow a \) cùng hướng với vecto \(\overrightarrow a \) và \(\left| {1\;\overrightarrow a } \right| = \left| {\overrightarrow a } \right|\).
Vậy hai vecto \(1\;\overrightarrow a \) và \(\overrightarrow a \) bằng nhau.
HĐ2
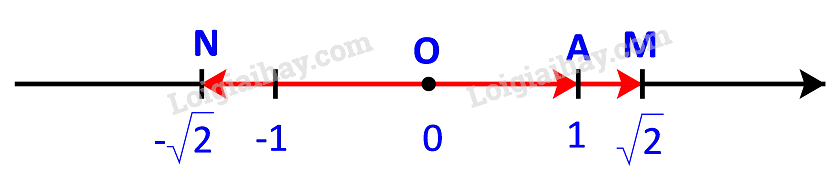
Trên một trục số, gọi O, A, M, N tương ứng biểu thị các số \(0;\;1;\;\sqrt 2 ;\; - \sqrt 2 \). Hãy nêu mối quan hệ về hướng và độ dài của mỗi vecto \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) với vecto \(\overrightarrow a = \overrightarrow {OA} \). Viết đẳng thức thể hiện mối quan hệ giữa hai vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \).
Phương pháp giải:
Vecto \(k\;\overrightarrow a \) (với \(k > 0,\;\overrightarrow a \ne \overrightarrow 0 \)) là vecto cùng hướng với vecto \(\overrightarrow a \) và có độ đài bằng \(k\;\left| {\overrightarrow a } \right|\).
Lời giải chi tiết:
Dễ thấy:
Vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \)có cùng giá nên chúng cùng phương.
Mà vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \)cùng nằm trên tia OM nên chúng cùng chiều
Vậy vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \)cùng hướng.
Ngoài ra, \(\left| {\overrightarrow {OM} } \right| = OM = \sqrt 2 \) và \(\left| {\overrightarrow {OA} } \right| = OA = 1\)
\( \Rightarrow \left| {\overrightarrow {OM} } \right| = \sqrt 2 .\left| {\overrightarrow {OA} } \right|\)
Ta kết luận \(\overrightarrow {OM} = \sqrt 2 .\overrightarrow {OA} \).
Câu hỏi
\( - \;\overrightarrow a \) và \( - 1\;\overrightarrow a \) có mối quan hệ gì?
Phương pháp giải:
Vecto \(k\;\overrightarrow a \) (với \(k < 0,\;\overrightarrow a \ne \overrightarrow 0 \)) là vecto ngược hướng với vecto \(\overrightarrow a \) và có độ đài bằng \(\left| k \right|\;\left| {\overrightarrow a } \right|\).
Lời giải chi tiết:
Ta có:
Vecto \( - \;\overrightarrow a \) là vecto đối của vecto \(\overrightarrow a \)
\( \Rightarrow - \;\overrightarrow a \) ngược hướng với vecto \(\overrightarrow a \) và \(\left| { - \;\overrightarrow a \;} \right| = \left| {\;\overrightarrow a \;} \right|\)
Lại có:
Vecto \( - 1\;\overrightarrow a \) là vecto ngược hướng với vecto \(\overrightarrow a \) và có độ đài bằng \(\left| { - 1} \right|\;\left| {\overrightarrow a } \right| = \left| {\overrightarrow a } \right|\).
\( \Rightarrow - \;\overrightarrow a \) và \( - 1\;\overrightarrow a \) cùng hướng và có độ dài bằng nhau (bằng vecto\(\;\overrightarrow a \)).
Hay \( - \;\overrightarrow a = - 1\;\overrightarrow a \)
Luyện tập 1
Cho đường thẳng d đi qua hai điểm phân biệt A và B. Những khẳng định nào sau đây là đúng?
a) Điểm M thuộc đường thẳng d khi và chỉ khi tồn tại số t để \(\overrightarrow {AM} = t.\overrightarrow {AB} \)
b) Với điểm M bất kì, ta luôn có \(\overrightarrow {AM} = \frac{{AM}}{{AB}}.\overrightarrow {AB} \)
c) Điểm M thuộc tia đối của tia AB khi và chỉ khi tồn tại số \(t \le 0\) để \(\overrightarrow {AM} = t.\overrightarrow {AB} \)
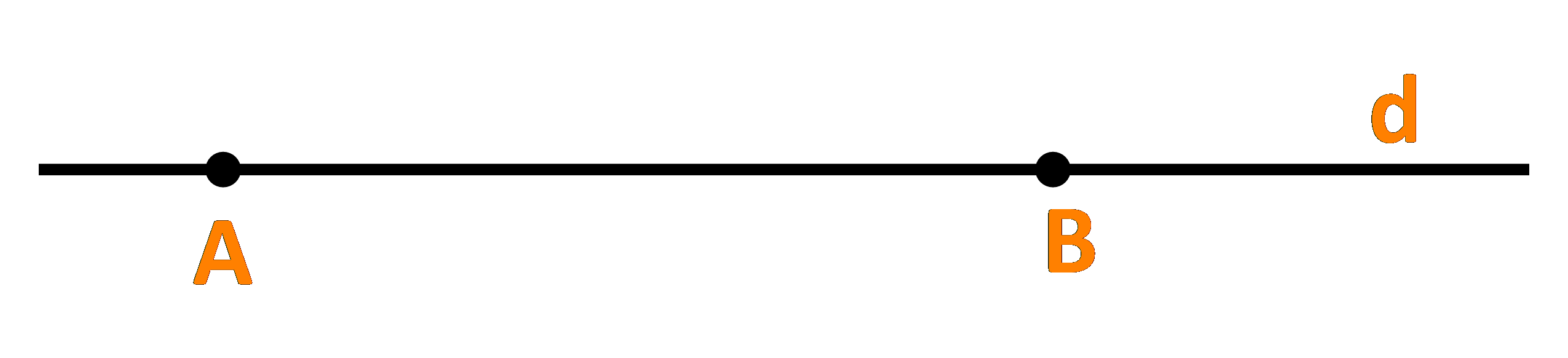
Phương pháp giải:
\(\overrightarrow a \) và \(\overrightarrow b \;\left( {\overrightarrow b \ne \overrightarrow 0 } \right)\) cùng phương khi và chỉ khi tồn tại số k để \(\overrightarrow a = k.\overrightarrow b \)
Nếu \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng thì \(k = \frac{{|\overrightarrow a |}}{{|\overrightarrow b |}}\)
Nếu \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng thì \(k = - \frac{{|\overrightarrow a |}}{{|\overrightarrow b |}}\)
Lời giải chi tiết:
a) Điểm M thuộc đường thẳng d khi và chỉ khi hai vecto \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) cùng phương (cùng giá d)
Khi và chỉ khi tồn tại số t để \(\overrightarrow {AM} = t.\overrightarrow {AB} \).
Vậy khẳng định a) đúng.
b) Với điểm M bất kì, ta luôn có \(\overrightarrow {AM} = \frac{{AM}}{{AB}}.\overrightarrow {AB} \)
Sai vì \(\overrightarrow {AM} = \frac{{AM}}{{AB}}.\overrightarrow {AB} \) khi và chỉ khi \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) cùng hướng.
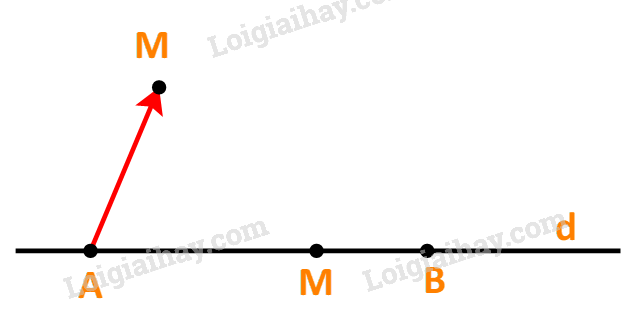
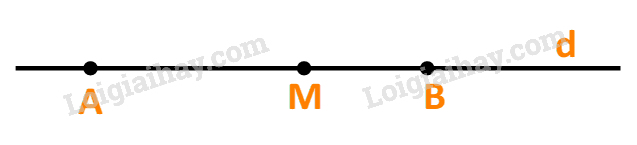
c) Điểm M thuộc tia đối của tia AB, tức là A nằm giữa M và B.
Khi và chỉ khi hai vecto \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) ngược hướng
\( \Leftrightarrow \) tồn tại số \(t \le 0\) để \(\overrightarrow {AM} = t.\overrightarrow {AB} \)
Vậy khẳng định c) đúng.


