Đề bài
Cho tứ giác ABCD. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh \(\overrightarrow {BC} + \overrightarrow {AD} = 2\overrightarrow {MN} = \;\overrightarrow {AC} + \overrightarrow {BD} .\)
Phương pháp giải - Xem chi tiết
+ Với ba điểm A, B, C bất kì ta luôn có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
+ M là trung điểm của đoạn AB thì \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 = \overrightarrow {AM} + \overrightarrow {BM} \)
Lời giải chi tiết
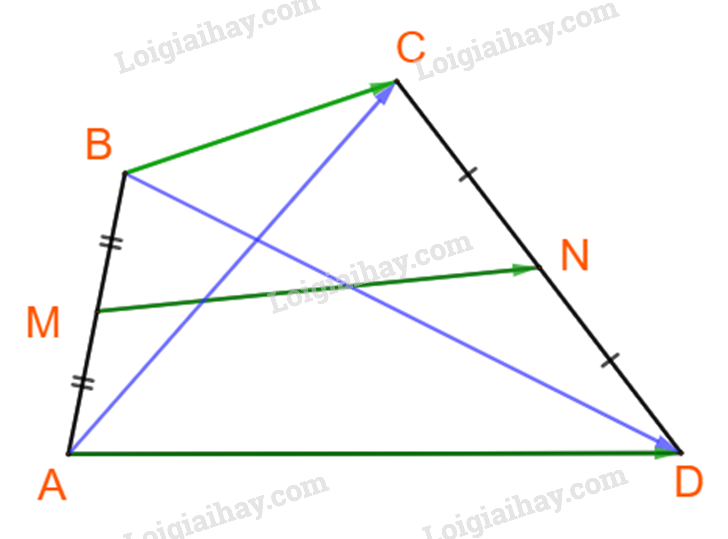
Ta có:
\(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} \)
Mặt khác: \(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} \)
\(\begin{array}{l} \Rightarrow 2\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} + \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} \\ \Leftrightarrow 2\overrightarrow {MN} = \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {DN} + \overrightarrow {CN} } \right) + \overrightarrow {BC} + \overrightarrow {AD} \\ \Leftrightarrow 2\overrightarrow {MN} = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow {BC} + \overrightarrow {AD} \\ \Leftrightarrow 2\overrightarrow {MN} = \overrightarrow {BC} + \overrightarrow {AD} \end{array}\)
Tương tự ta cũng có:
\(\left\{ \begin{array}{l}\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AC} + \overrightarrow {CN} \\\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BD} + \overrightarrow {DN} \end{array} \right.\)
\(\begin{array}{l} \Rightarrow 2\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AC} + \overrightarrow {CN} + \overrightarrow {MB} + \overrightarrow {BD} + \overrightarrow {DN} \\ \Leftrightarrow 2\overrightarrow {MN} = \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {CN} + \overrightarrow {DN} } \right) + \overrightarrow {AC} + \overrightarrow {BD} \\ \Leftrightarrow 2\overrightarrow {MN} = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow {AC} + \overrightarrow {BD} \\ \Leftrightarrow 2\overrightarrow {MN} = \overrightarrow {AC} + \overrightarrow {BD} \end{array}\)
Vậy \(\overrightarrow {BC} + \overrightarrow {AD} = 2\overrightarrow {MN} = \;\overrightarrow {AC} + \overrightarrow {BD} .\)

