Đề bài
Cho định lí: “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Mệnh đề nào sau đây là đúng?
A. Hai tam giác bằng nhau là điều kiện cần để diện tích của chúng bằng nhau.
B. Hai tam giác bằng nhau là điều kiện cần và đủ để diện tích của chúng bằng nhau
C. Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau
D. Hai tam giác bằng nhau là điều kiện đủ để diện tích của chúng bằng nhau
Phương pháp giải - Xem chi tiết
“P là điều kiện đủ để có Q” hoặc “Q là điều kiện cần để có P” nếu mệnh đề \(P \Rightarrow Q\) đúng.
“P là điều kiện cần và đủ để có Q” nếu mệnh đề \(P \Leftrightarrow Q\) đúng.
Lời giải chi tiết
Xét hai mệnh đề:
P: “Hai tam giác bằng nhau”
Q: “Hai tam giác có diện tích bằng nhau”
A. Hai tam giác bằng nhau là điều kiện cần để diện tích của chúng bằng nhau.
Mệnh đề “P là điều kiện cần để có Q”. Ta kiểm tra mệnh đề \(Q \Rightarrow P\)
Dễ thấy “Hai tam giác có diện tích bằng nhau” không suy ra “Hai tam giác bằng nhau”
Chẳng hạn: \(\Delta ABC\) và \(\Delta DEF\)đều có diện tích \(\left( {12\;c{m^2}} \right)\) nhưng chúng không bằng nhau.
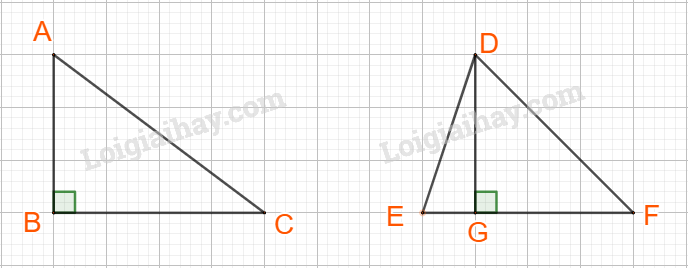
Vậy mệnh đề \(Q \Rightarrow P\) sai.
Đáp án A sai
B. Hai tam giác bằng nhau là điều kiện cần và đủ để diện tích của chúng bằng nhau
Mệnh đề “P là điều kiện cần và đủ để có Q”. Ta kiểm tra mệnh đề \(P \Leftrightarrow Q\)
Vì \(Q \not{\Rightarrow}P\) nên \(P\not{ \Leftrightarrow }Q\)
Vậy mệnh đề \(P \Leftrightarrow Q\)sai
Đáp án B sai
C. Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau
Mệnh đề “Q là điều kiện đủ để có P”. Ta kiểm tra mệnh đề \(Q \Rightarrow P\)
Theo ý A, mệnh đề \(Q \Rightarrow P\) sai.
Vậy đáp án C sai
D. Hai tam giác bằng nhau là điều kiện đủ để diện tích của chúng bằng nhau
Mệnh đề “P là điều kiện đủ để có Q”. Ta kiểm tra mệnh đề \(P \Rightarrow Q\)
Dễ thấy “Hai tam giác bằng nhau” thì (hiển nhiên) suy ra“Hai tam giác có diện tích bằng nhau”
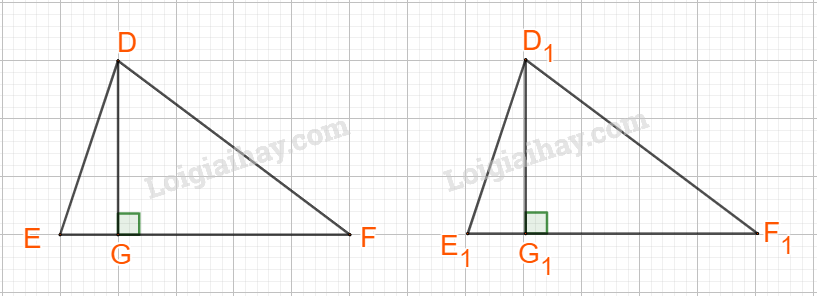
Vậy mệnh đề \(P \Rightarrow Q\) đúng.
Đáp án D đúng.
Chọn đáp án D.

