Luyện tập 3
Giải tam giác ABC, biết b = 32, c =45, ˆA=87o
Phương pháp giải:
Tính độ dài các cạnh và các góc còn lại của tam giác.
Bước 1: Tính a: a2=b2+c2−2.bc.cosA
Bước 2: Tính sinB, suy ra góc B, góc C.
Lời giải chi tiết:
Ta cần tính cạnh BC, góc B và góc C.
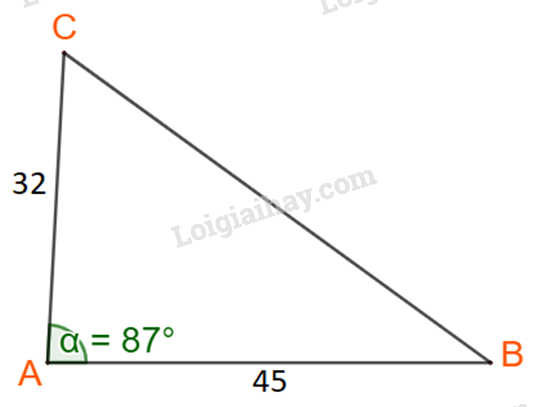
Áp dụng định lí cosin tại đỉnh A ta có:
a2=b2+c2−2bc.cosA
⇔BC2=322+452−2.32.45.cos87o⇔BC2≈2898,27⇔BC≈53,8
Theo định lí sin, ta có:
asinA=bsinB⇒sinB=b.sinAa=32.sin87o53,8≈0,594.
⇒ˆB≈36,44o hoặc ˆB≈143,56o(Loại vì ˆA+ˆB=230,56o>180o)
⇒ˆC=180o−ˆA−ˆB≈180o−87o−36,44o=56,56o
Vậy tam giác ABC có BC≈53,8; ˆB≈36,44o và ˆC=56,56o.
Vận dụng 2
Từ một khu vực có thể quan sát được hai đỉnh núi, ta có thể ngắm và đo để xác định khoảng cách giữa hai đỉnh núi đó. Hãy thảo luận để đưa ra các bước cho một cách đo.
Phương pháp giải:
Bước 1: Cố định vị trí đứng ngắm, xác định góc ngắm .
Bước 2: Đo khoảng cách từ vị trí ngắm tới từng đỉnh núi..
Bước 3: Áp dụng định lí cosin để xác định khoảng cách giữa hai đỉnh núi.
Lời giải chi tiết:
Bước 1: Tại khu vực quan sát, đặt một cọc tiêu cố định tại vị trí A. Kí hiệu hai đỉnh núi lần lượt là điểm B và điểm C.
+) Đứng tại A, ngắm điểm B và điểm C để đo góc tạo bởi hai hướng ngắm đó.
Bước 2: Đo khoảng cách từ vị trí ngắm đến từng đỉnh núi, tức là tính AB, AC.
- Tính AB bằng cách:
+) Đứng tại A, ngắm đỉnh núi B để xác định góc ngắm so với mặt đất, kí hiệu là góc α.
+) Theo hướng ngắm, đặt tiếp cọc tiêu tại D gần đỉnh núi hơn và đo đoạn AD. Xác định góc ngắm tại điểm D, kí hiệu là gócβ
Hình vẽ:
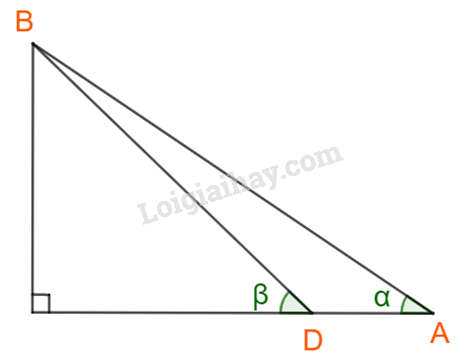
Dễ dàng tính được góc ^DBA=180o−α−β.
Áp dụng định lí sin cho tam giác ABD ta được: ABsinD=DAsinB⇒AB=sinD.DAsinB=sin(180o−β).DAsin(180o−α−β).
- Làm tương tự để tính AC.
Bước 3: Tính khoảng cách giữa hai đỉnh núi, bằng cách áp dụng định lí cosin cho tam giác ABC để tính độ dài cạnh BC.
