HĐ3
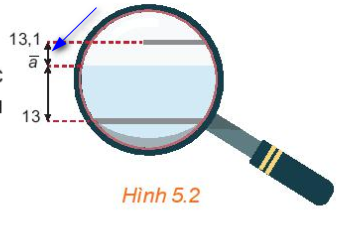
Trong HĐ2, Hòa dùng kính lúp để quan sát mực nước trên ống đo thứ hai được hình ảnh như Hình 5.2. Kí hiệu \(\overline a \)(\(c{m^3}\)) là số đo thể tích của nước.
Quan sát hình vẽ để so sánh \(\left| {13 - \bar a} \right|\) và \(\left| {13,1 - \bar a} \right|\) rồi cho biết trong hai số đo thể tích \(13c{m^3}\) và \(13,1c{m^3}\), số đo nào gần với thể tích của cốc nước hơn.
Phương pháp giải:
Quan sát hình vẽ 5.2 và kiểm tra giữa hai số 13,1 và 13, số nào gần \(\bar a\) hơn.
Lời giải chi tiết:
Ta quan sát hình trên thì thấy số 13,1 gần \(\bar a\) hơn.
Luyện tập 2
Một phép đo đường kính nhân tế bào cho kết quả là \(5 \pm 0,3\mu m\). Đường kính thực của nhân tế bào thuộc đoạn nào?
Phương pháp giải:
Ta viết \(\bar a = a \pm d\) thì có nghĩa là số đúng \(\bar a\) nằm trong đoạn \(\left[ {a - d;a + d} \right]\).
Với a là số gần đúng của \(\bar a\) và d là độ chính xác của \(\bar a\).
Lời giải chi tiết:
Gọi \(\bar a\) là đường kính thực của nhân tế bào.
Vì phép đo đường kính nhân tế bào cho kết quả là \(5 \pm 0,3\mu m\).
=> \(a = 5\mu m;d = 0,3\mu m\)
Nên ta có \(\bar a\) nằm trong đoạn \(\left[ {5 - 0,3;5 + 0,3} \right]\) hay \(\left[ {4,7;5,3} \right]\).
HĐ4

Công ty (trong Ví dụ 2) cũng sử dụng dây chuyền B để đóng gạo với khối lượng chính xác là 20 kg. Trên bao bì ghi thông tin khối lượng là \(20 \pm 0,5\) kg.
Khẳng định “Dây chuyền A tốt hơn dây chuyền B" là đúng hay sai?
Lời giải chi tiết:
Mặc dù độ chính xác của khối lượng bao gạo đóng bằng dây chuyền A nhỏ hơn nhưng do bao gạo đóng bằng dây chuyền B nặng hơn nhiều nên ta không dựa vào sai số tuyệt đối để so sánh.
Do đó câu hỏi này ta chưa thể trả lời chính xác được nếu chỉ dựa vào các kiến thức đã học trước đó.
Xem thêm bài Luyện tập 3 trang 76 Sách giáo khoa Toán 10 – Kết nối tri thức với cuộc sống.
Luyện tập 3
Đánh giá sai số tương đối của khối lượng bao gạo được đóng gói theo hai dây chuyền A, B ở Ví dụ 2 và HĐ4. Dựa trên tiêu chí này, dây chuyền nào tốt hơn?
Phương pháp giải:
- Đánh giá sai số tương đối: \({\delta _a} \le \frac{d}{{\left| a \right|}}\)
Với d là độ chính xác và a là số gần đúng.
- Nhận xét dây chuyền nào tốt hơn: \(\frac{d}{{\left| a \right|}}\) càng nhỏ thì chất lượng phép đo hay tính toán càng cao.
Lời giải chi tiết:
Xét dây chuyền A: ta có d=0,2; a=5.
\({\delta _5} \le \frac{{0,2}}{{\left| 5 \right|}} = 0,04 = 4\% \)
Xét dây chuyền B: ta có d=0,5; a=20
\({\delta _5} \le \frac{{0,5}}{{\left| {20} \right|}} = 0,025 = 2,5\% \)
Ta thấy \(2,5\% < 4\% \) nên dây chuyền B tốt hơn.
Chú ý
Có thể không cần đổi sang đơn vị phần trăm (%) để so sánh.

