HĐ3
Trong mỗi hình dưới dây, hãy tính R theo a và sinA.
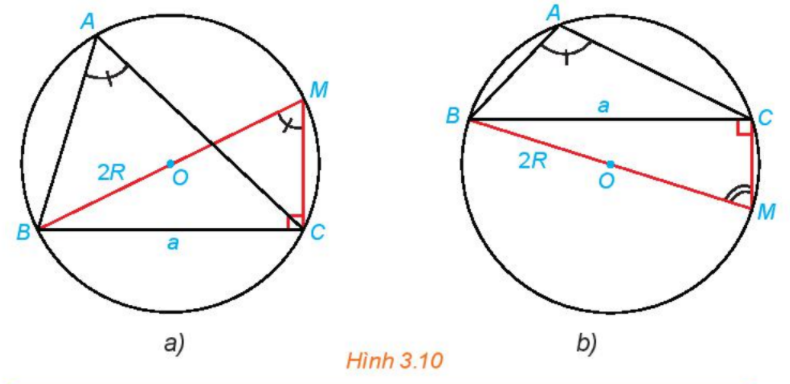
Phương pháp giải:
Bước 1: Tính sin M. Từ đó tính R theo a và sinM.
Bước 2: Tìm mối liên hệ giữa sinA và sinM, suy ra công thức tính R theo sinA.
Lời giải chi tiết:
Xét tam giác MBC vuông tại C ta có:
\(\sin M = \dfrac{{BC}}{{BM}} = \dfrac{a}{{2R}} \Rightarrow R = \dfrac{a}{{2\sin M}}\)
Lại có: Hình 3.10 a: \(\widehat A = \widehat M\) (cùng chắn cung nhỏ BC )
\( \Rightarrow \sin A = \sin M \Rightarrow R = \dfrac{a}{{2\sin A}}\)
Hình 3.10b: \(\widehat A + \widehat M = {180^o}\) (cùng tứ giác ABMC nội tiếp đường tròn (O,R))
\( \Rightarrow \sin A = \sin M \Rightarrow R = \dfrac{a}{{2\sin A}}\)
Vậy ở cả hai hình ta đều có: \(R = \dfrac{a}{{2\sin A}}\).
Luyện tập 2
Cho tam giác ABC có b = 8, c = 5 và \(\widehat B = {80^o}\). Tính số đo các góc, bán kính đường tròn ngoại tiếp và độ dài cạnh còn lại của tam giác.
Phương pháp giải:
Bước 1: Tính sin\(\widehat C\), bằng cách áp dụng định lí sin tại đỉnh B và C. Từ đó suy ra số đo góc C.
Bước 2: Tính \(\widehat A\) và suy ra a dựa vào định lí sin.
Bước 3: Tính R.
Lời giải chi tiết:
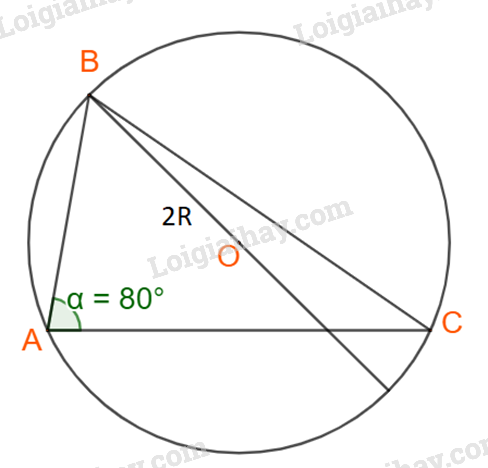
Áp dụng định lí sin cho tam giác ABC ta có:
\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R\)
\(\begin{array}{l} \Rightarrow \sin C = \frac{{c.\sin B}}{b} = \frac{{5.\sin {{80}^o}}}{8} \approx 0,6155\\ \Leftrightarrow \widehat C \approx {38^o}\end{array}\)
Lại có: \(\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {80^o} - {38^o} = {62^o}\)
Theo định lí sin, ta suy ra \(a = \sin A.\dfrac{b}{{\sin B}} = \sin {62^o}\dfrac{8}{{\sin {{80}^o}}} \approx 7,17\)
Và \(2R = \dfrac{b}{{\sin B}} \Rightarrow R = \dfrac{b}{{2\sin B}} = \dfrac{8}{{2\sin {{80}^o}}} \approx 4,062.\)
Vậy tam giác ABC có \(\widehat A = {62^o}\); \(\widehat C \approx {38^o}\); \(a \approx 7,17\) và \(R \approx 4,062.\)

