HĐ1
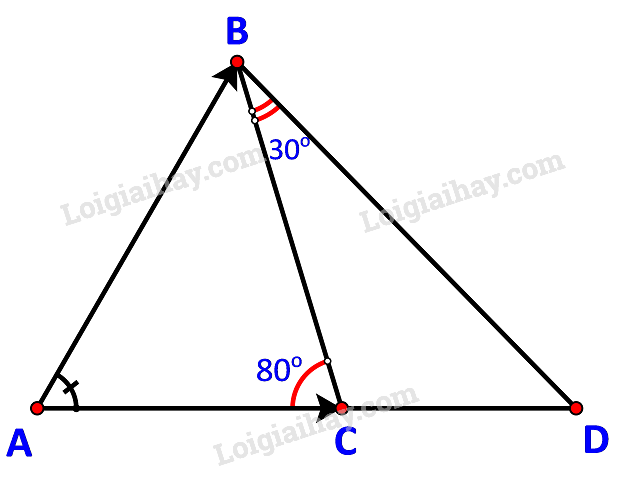
Trong hình 4.39, số đo góc BAC cũng được gọi là số đo góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \). Hãy tìm số đo các góc giữa \(\overrightarrow {BC} \) và \(\overrightarrow {BD} \), \(\overrightarrow {DA} \) và \(\overrightarrow {DB} \).
Lời giải chi tiết:
Góc giữa hai vectơ \(\overrightarrow {BC} \) và \(\overrightarrow {BD} \) là góc CBD và số đo \(\widehat {CBD} = {30^o}\).
Góc giữa hai vectơ \(\overrightarrow {DA} \) và \(\overrightarrow {DB} \) là góc ADB.
Ta có: \(\widehat {ACB} = \widehat {CBD} + \widehat {CDB}\) (tính chất góc ngoài)
\(\begin{array}{l} \Leftrightarrow \widehat {CDB} = {80^o} - {30^o} = {50^o}\\ \Leftrightarrow \widehat {ADB} = {50^o}\end{array}\)
Vậy số đo góc giữa hai vectơ \(\overrightarrow {BC} \) và \(\overrightarrow {BD} \), \(\overrightarrow {DA} \) và \(\overrightarrow {DB} \) lần lượt là \({30^o},{50^o}\)
Câu hỏi
Khi nào thì góc giữa hai vectơ bằng \({0^o}\), bằng \({180^o}?\)
Phương pháp giải:
Cách xác định góc giữa hai vecto \(\overrightarrow u ,\overrightarrow v \)
Lấy điểm A bất kì vẽ \(\overrightarrow {AB} = \overrightarrow u ,\overrightarrow {AC} = \overrightarrow v \), khi đó \((\vec u,\vec v) = (\overrightarrow {AB} ,\overrightarrow {AC} ) = \widehat {BAC}\)
Lời giải chi tiết:
Góc giữa hai vectơ bằng \({0^o}\) nếu chúng cùng hướng
Góc giữa hai vectơ bằng \({180^o}\) nếu chúng ngược hướng.
Luyện tập 1
Cho tam giác đều ABC. Tính \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right)\).
Phương pháp giải:
Lấy D sao cho: \(\overrightarrow {AD} = \overrightarrow {BC} \).
Khi đó: \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = \widehat {BAD}\)
Lời giải chi tiết:
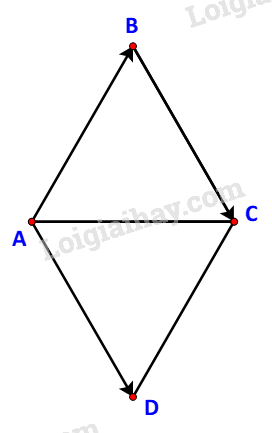
Lấy điểm D sao cho: \(\overrightarrow {AD} = \overrightarrow {BC} \)
Khi đó ta có: \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = \widehat {BAD}\)
Dễ thấy ABCD là hình bình hành (hơn nữa còn là hình thoi) nên \(\widehat {BAD} = {180^o} - \widehat {ABC} = {120^o}\)
Vậy số đo góc \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right)\) là \({120^o}\).