HĐ1
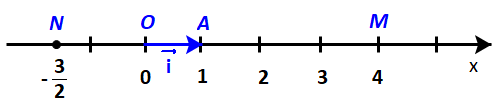
Trên trục số Ox, gọi A là điểm biểu diễn số 1 và đặt \(\overrightarrow {OA} = \overrightarrow i \) (H.4.32a). Gọi M là điểm biểu diễn số 4, N là điểm biểu diễn số \( - \frac{3}{2}\). Hãy biểu thị mỗi vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) theo vectơ \(\overrightarrow i \).
Phương pháp giải:
+) \(\overrightarrow a = k.\overrightarrow b ,\quad (k > 0) \Leftrightarrow \) Vecto \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng, \(\left| {\overrightarrow a } \right| = k.\left| {\overrightarrow b } \right|\quad (k > 0)\)
+) \(\overrightarrow a = k.\overrightarrow b ,\quad (k < 0) \Leftrightarrow \) Vecto \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng, \(\left| {\overrightarrow a } \right| = - k.\left| {\overrightarrow b } \right|\quad (k < 0)\)
(\(\overrightarrow b \ne \overrightarrow 0 \))
Lời giải chi tiết:
Dễ thấy:
vectơ \(\overrightarrow {OM} \) cùng hướng với vectơ \(\overrightarrow i \) và \(\left| {\overrightarrow {OM} } \right| = 4 = 4\left| {\overrightarrow i } \right|\)
Do đó: \(\overrightarrow {OM} = 4\,.\,\overrightarrow i \)
Tương tự, vectơ \(\overrightarrow {ON} \) ngược hướng với vectơ \(\overrightarrow i \) và \(\left| {\overrightarrow {ON} } \right| = \frac{3}{2} = \frac{3}{2}\left| {\overrightarrow i } \right|\)
Do đó: \(\overrightarrow {ON} = - \frac{3}{2}\,.\,\overrightarrow i \)
HĐ2
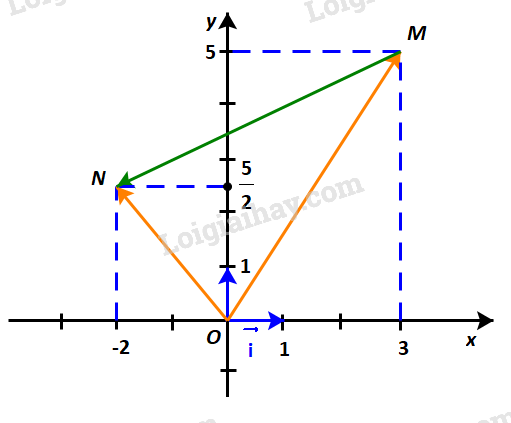
Trong Hình 4.33:
a) Hãy biểu thị mỗi vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \).
b) Hãy biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) từ đó biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \).
Phương pháp giải:
a) Quy tắc hình bình hành:
Tứ giác OAMB là hình bình hành thì \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \)
b) Quy tắc hiệu: \(\overrightarrow {MN} = \overrightarrow {ON} - \;\overrightarrow {OM} \)
Lời giải chi tiết:
Dựng hình bình hành OAMB và OCND như hình dưới:

Khi đó: \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \) và \(\overrightarrow {ON} = \overrightarrow {OC} + \overrightarrow {OD} \).
Dễ thấy:
\(\overrightarrow {OA} = 3\;\overrightarrow i ;\;\,\overrightarrow {OB} = 5\;\overrightarrow j \) và \(\overrightarrow {OC} = - 2\;\overrightarrow i ;\;\,\overrightarrow {OD} = \frac{5}{2}\;\overrightarrow j \)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {OM} = 3\;\overrightarrow i + 5\;\overrightarrow j \\\overrightarrow {ON} = - 2\;\overrightarrow i + \frac{5}{2}\;\overrightarrow j \end{array} \right.\)
b) Ta có: \(\overrightarrow {MN} = \overrightarrow {ON} - \;\overrightarrow {OM} \) (quy tắc hiệu)
\(\begin{array}{l} \Rightarrow \overrightarrow {MN} = \left( { - 2\;\overrightarrow i + \frac{5}{2}\;\overrightarrow j } \right) - \left( {\;3\;\overrightarrow i + 5\;\overrightarrow j } \right)\\ \Leftrightarrow \overrightarrow {MN} = \left( { - 2\;\overrightarrow i - 3\;\overrightarrow i } \right) + \left( {\frac{5}{2}\;\overrightarrow j - 5\;\overrightarrow j } \right)\\ \Leftrightarrow \overrightarrow {MN} = - 5\;\overrightarrow i - \frac{5}{2}\;\overrightarrow j \end{array}\)
Vậy \(\overrightarrow {MN} = - 5\;\overrightarrow i - \frac{5}{2}\;\overrightarrow j \).
Luyện tập 1
Tìm tọa độ của \(\overrightarrow 0 \)
Lời giải chi tiết:
Vì: \(\overrightarrow 0 = 0.\;\overrightarrow i + 0.\;\overrightarrow j \) nên \(\overrightarrow 0 \) có tọa độ là (0;0).

