HĐ1
Trong tình huống trên, gọi A là tập hợp những thành viên tham gia chuyên đề 1, B là tập hợp những thành viên tham gia chuyên đề 2.
a) Nam có là một phần tử của tập hợp A không? Ngân có là một phần tử của tập hợp B không?
b) Hãy mô tả các tập hợp A và B bằng cách liệt kê các phần tử.
Phương pháp giải:
a) Nếu Nam có tên trong màn hình của chuyên đề 1 thì Nam là một phần tử của tập hợp A và ngược lại.
b) Viết tập hợp A, B bằng cách liệt kê các phần tử.
Lời giải chi tiết:

a) Nam có là một phần tử của tập hợp A
Ngân không là một phần tử của tập hợp B
b) \(A = \){Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
\(B = \){Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
HĐ2
Cho tập hợp:
C = {châu Á; châu Âu; châu Đại Dương; châu Mĩ; châu Nam Cực; châu Phi}.
a) Hãy chỉ ra tính chất đặc trưng cho các phần tử của tập hợp C.
b) Tập hợp C có bao nhiêu phần tử?
Lời giải chi tiết:
a) Tính chất đặc trưng của các phần tử của tập hợp C: là các châu lục trên Trái đất.
b) Tập hợp C có 6 phần tử.
Luyện tập 1
Gọi S là tập nghiệm của phương trình \({x^2} - 24x + 143 = 0\).
Các mệnh đề sau đúng hay sai?
a) \(13 \in S\)
b) \(11 \notin S\)
c) \(n\;(S) = 2\)
Lời giải chi tiết:
a) Vì \({13^2} - 24.13 + 143 = 0\) nên \(x = 13\) là nghiệm của phương trình \( \Rightarrow 13 \in S\)
Vậy mệnh đề “\(13 \in S\)” đúng.
b) Vì \({11^2} - 24.11 + 143 = 0\) nên \(x = 11\) là nghiệm của phương trình \( \Rightarrow 11 \in S\)
Vậy mệnh đề “\(11 \notin S\)” sai.
c) Ta có:
\(\begin{array}{l}{x^2} - 24x + 143 = 0\\ \Leftrightarrow {x^2} - 11x - 13x + 11.13 = 0\\ \Leftrightarrow x.\left( {x - 11} \right) - 13.\left( {x - 11} \right) = 0\\ \Leftrightarrow \left( {x - 11} \right).\left( {x - 13} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 11\\x = 13\end{array} \right.\end{array}\)
Vậy phương trình có 2 nghiệm hay \(n\;(S) = 2\)
Mệnh đề “\(n\;(S) = 2\)” đúng.
HĐ3
Gọi H là tập hợp các bạn tham gia Chuyên đề 2 trong tình huống mở đầu có tên bắt đầu bằng chữ chữ H. Các phần tử của tập hợp H có là phần tử của tập hợp B trong HĐ 1 không?

Lời giải chi tiết:
Ta có: \(B = \){Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
và H = {Hương; Hiền; Hân}
Vậy các phần tử của H đều là phần tử của tập hợp B.
HĐ4
Sơn và Thu viết tập hợp các số chính phương nhỏ hơn 100 như sau:
Sơn: {0; 1; 4; 9; 16; 25; 36; 49; 64; 81};
Thu: T = { \(n \in \mathbb{N}\) | n là số chính phương; \(n < 100\)}.
Hỏi bạn nào viết đúng?
Phương pháp giải:
Có thể mô tả một tập hợp bằng một trong hai cách:
Cách 1: Liệt kê các phần tử của tập hợp;
Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.
Lời giải chi tiết:
Cả hai bạn viết đều đúng.
Sơn viết theo cách liệt kê các phần tử (số chính phương nhỏ hơn 100).
Còn Thu viết tập hợp theo cách chỉ ra tính chất đặc trưng (số chính phương và nhỏ hơn 100).
Luyện tập 2
Giả sử C là tập hợp các hình bình hành có hai đường chéo vuông góc; D là tập hợp các hình vuông.
Các mệnh đề sau đúng hay sai?
a) \(C \subset D\);
b) \(C \supset D\);
c) \(C = D\).
Phương pháp giải:
Mô tả tập hợp C và tập hợp D.
So sánh các phần tử của hai tập hợp.
Lời giải chi tiết:
+) Mô tả tập hợp D = {các hình vuông}
+) Mô tả tập hợp C = {các hình bình hành có hai đường chéo vuông góc} = {Các hình thoi}.
Thật vậy,
Xét tứ giác ABCD, là hình hình hành có hai đường chéo vuông góc.
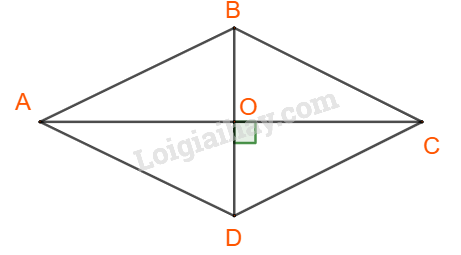
Gọi \(AC \cap BD = O\) thì O là trung điểm của AC và BD.
Ta có: AO vừa là trung tuyến vừa là đường cao.
\( \Rightarrow \Delta ABD\) cân tại A.
\( \Rightarrow AB = AD\).
Tương tự ta cũng có: \(CB = CD\).
Mà \(AB = CD;\;AD = BC\).
Do đó: \(AB = CD = \;AD = BC\) hay tứ giác ABCD là hình thoi.
a) Vì nhiều hình thoi (các hình thoi không có góc nào vuông) thì không phải là hình vuông, nên \(C\not{ \subset }D\).
Vậy mệnh đề “\(C \subset D\)” sai.
b) Vì mỗi hình vuông cũng là một hình thoi (hình thoi đặc biệt: có một góc vuông), nên các phần tử của D cũng là phần tử của D. Hay \(C \supset D\)
Do đó mệnh đề “\(C \supset D\)” đúng.
c) Vì \(\left\{ \begin{array}{l}C \subset D\\C \supset D\end{array} \right.\;\; \Rightarrow C \ne D\)
Vậy mệnh đề “\(C = D\)” sai.

