HĐ1
Một tàu biển xuất phát từ cảng Vân Phong (Khánh Hòa) theo hướng đông với vận tốc 20km/h. Sau khi đi được 1 giờ, tàu chuyển sang hướng đông nam rồi giữ nguyên vận tốc và đi tiếp.
a) Hãy vẽ sơ đồ đường đi của tàu trong 1,5 giờ kể từ khi xuất phát (1km trên thực tế ứng với 1 cm trên bản vẽ).
b) Hãy đo trực tiếp trên bản vẽ và cho biết sau 1,5 giờ kể từ khi xuất phát, tàu cách cảng Vân Phong bao nhiêu kilomet (số đo gần đúng).
c) Nếu sau khi đi được 2 giờ, tàu chuyển sang hướng nam (thay vì hướng đông nam) thì có thể dùng định lí Pythagore (Pi-ta-go) để tính chính xác các số đo trong câu b hay không?
Phương pháp giải:
a)
Bước 1: Xác định các hướng Đông, tây, nam, bắc. Giả sử tàu xuất phát từ điểm O.
Bước 2: Tính quãng đường đi theo từng hướng sau 1,5 giờ.
Bước 3: Vẽ sơ đồ đường đi
b)
Bước 1: Đo khoảng cách từ điểm xuất phát tới tàu trên sơ đồ
Bước 2: Quy ra khoảng cách thực tế.
c)
Bước 1: Vẽ sơ đồ đường đi.
Bước 2: Tính khoảng cách từ cảng tới tàu dựa vào định lí Pythagore.
Lời giải chi tiết:
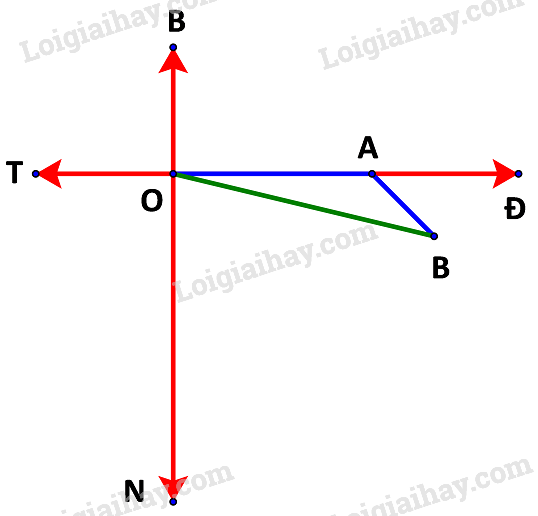
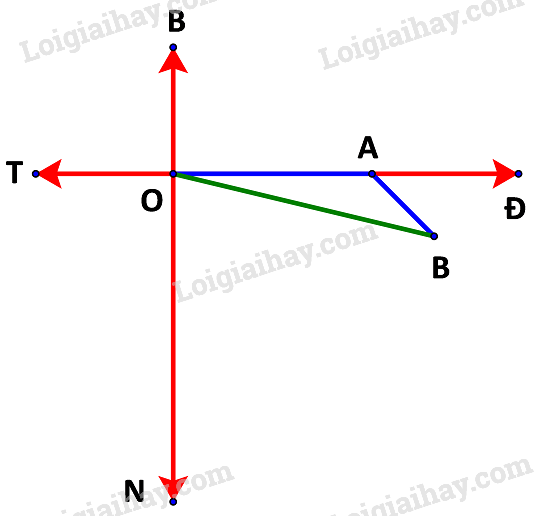
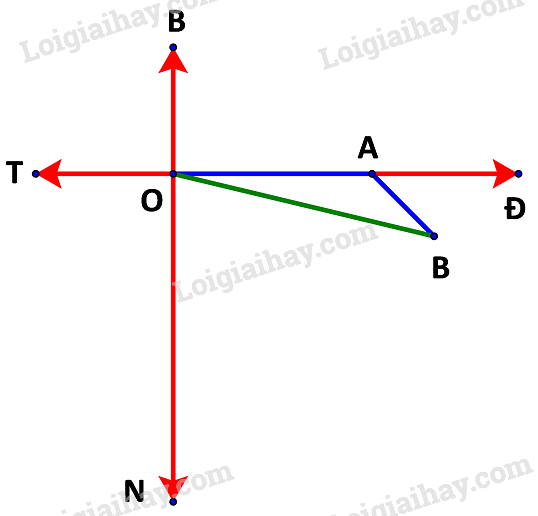
a) Giả sử tàu xuất phát từ điểm O như hình dưới.
Trong 1 giờ, tàu di chuyển từ O đến A với quãng đường là: 20.1 =20 (km) tương ứng với 20 cm trên sơ đồ.
Trong 0,5 giờ tiếp theo, tàu di chuyển từ A đến B với quãng đường là: 20.0,5 = 10 (km) tương ứng với 10 cm trên sơ đồ.
b)
Trên sơ đồ, khoảng cách từ cảng đến tàu là đoạn OB dài khoảng 28 cm
Do đó khoảng cách từ cảng đến tàu thực tế khoảng 28 km.
c)
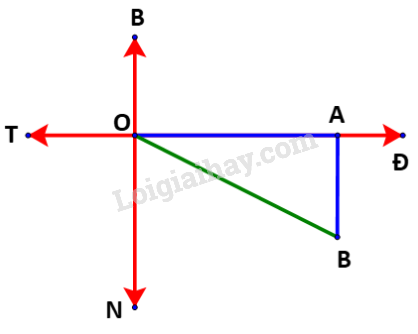
Nếu sau khi đi được 2 giờ, tàu chuyển sang hướng nam (thay vì hướng đông nam) thì sơ đồ đường đi của tàu như sau:
Sau 2 giờ đầu, tàu đi từ O đến A, với quãng đường là 20.2 = 40 (km) tương ứng 40 cm trên sơ đồ.
Sau đó, tàu chuyển sang hướng nam, vị trí của tàu là điểm B.
Khi đó ta có thể tính chính xác khoảng cách từ cảng đến tàu, chính là đoạn OB (do tam giác OAB vuông tại A) dựa vào định lí Pythagore: \(OB = \sqrt {O{A^2} + A{B^2}} \)
HĐ2
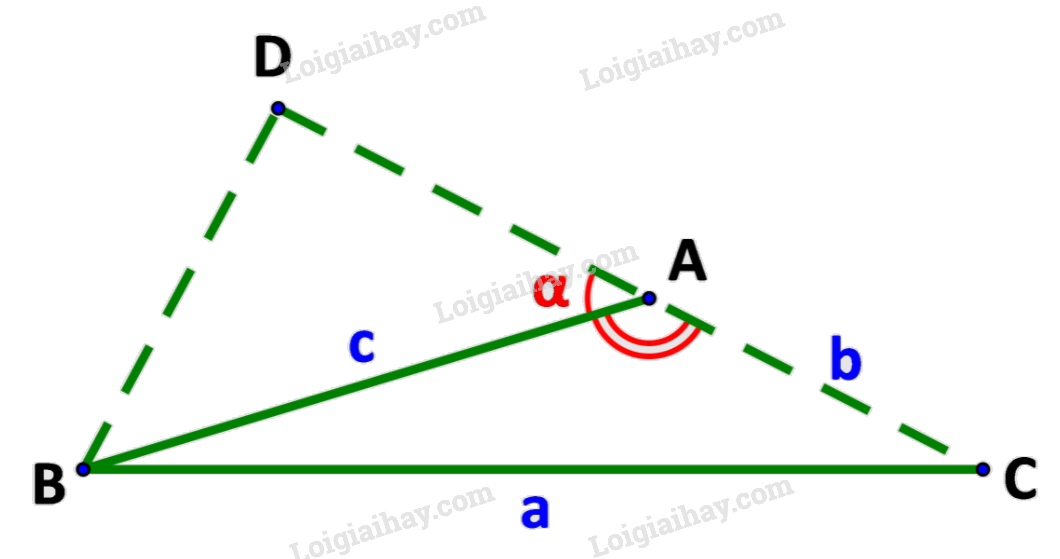
Trong Hình 3.8, hãy thực hiện các bước sau để thiết lập công thức tính a theo b,c và giá trị lượng giác của góc A
a) Tính \({a^2}\) theo \(B{D^2}\) và \(C{D^2}\)
b) Tính \({a^2}\) theo b, c và DA.
c) Tính DA theo c và \(\cos A\).
d) Chứng minh \({a^2} = {b^2} + {c^2} - 2bc\;\cos A.\)
Phương pháp giải:
a) Áp dụng định lí Pythagore với tam giác BCD.
b) Bước 1: Tính BD theo DA và c (định lí Pythagore cho tam giác BDA)
Bước 2: Thay DC bởi DA + b.
Bước 3: Thế BD và DC ở trên vào biểu thức ở ý a)
c)
Bước 1: Tính \(\cos A\) theo \(\cos \alpha \).
Bước 2: Tính DA theo c và \(\cos \alpha \)
Bước 3: Suy ra công thức tính DA theo c và \(\cos A\)
d)
Lời giải chi tiết:
a) Xét tam giác BDC vuông tại D, theo định lý Pythagore ta có:
\({a^2} = B{D^2} + D{C^2}\) (1)
b) Xét tam giác vuông BDA ta có:
\(\left\{ \begin{array}{l}B{A^2} = B{D^2} + D{A^2} \Rightarrow B{D^2} = B{A^2} - D{A^2} = {c^2} - D{A^2}\\\cos \alpha = \frac{{DA}}{c} \Rightarrow DA = c.\cos \alpha \end{array} \right.\)
Lại có: DC = DA + AC = DA + b Thế vào (1)
\( \Rightarrow {a^2} = \left( {{c^2} - D{A^2}} \right) + {\left( {DA + b} \right)^2}\) (2)
c) Xét tam giác vuông BDA ta có:
\(\cos \alpha = \frac{{DA}}{c} \Rightarrow DA = c.\cos \alpha \)
Mà \(\cos \alpha = - \cos A\) (do góc \(\alpha \) và góc A bù nhau)
\( \Rightarrow DA = - \,\,c.\cos A\)
d) Thế \(DA = - \,\,c.\cos A\) vào (2) ta được:
\(\begin{array}{l}{a^2} = \left[ {{c^2} - {{\left( { - \,\,c.\cos A} \right)}^2}} \right] + {\left( { - \,\,c.\cos A + b} \right)^2}\\ \Leftrightarrow {a^2} = \left( {{c^2} - \,\,{c^2}.{{\cos }^2}A} \right) + \left( {{c^2}.{{\cos }^2}A - \,2b\,c.\cos A + {b^2}} \right)\\ \Leftrightarrow {a^2} = {c^2} - \,\,{c^2}.{\cos ^2}A + {c^2}.{\cos ^2}A - \,2b\,c.\cos A + {b^2}\\ \Leftrightarrow {a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\end{array}\) (đpcm)
Câu hỏi
Định lí Pythagore có phải là một trường hợp đặc biệt của định lí cosin hay không?
Lời giải chi tiết:
Theo định lí cosin ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\\{b^2} = {a^2} + {c^2} - \,2a\,c.\cos B\\{c^2} = {b^2} + {a^2} - \,2ab.\cos C\end{array}\)
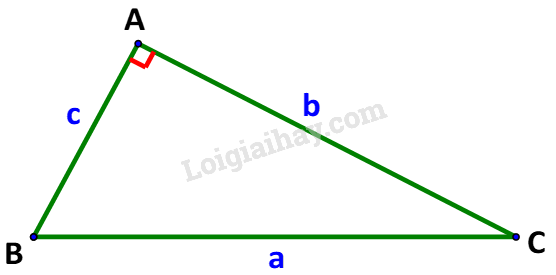
Mà \(\cos A = \cos {90^o} = 0;\cos B = \frac{c}{a};\;\cos C = \frac{b}{a}\)
\( \Rightarrow \left\{ \begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.0\\{b^2} = {a^2} + {c^2} - \,2a\,c.\frac{c}{a}\\{c^2} = {b^2} + {a^2} - \,2ab.\frac{b}{a}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{a^2} = {b^2} + {c^2}\\{b^2} = {a^2} + {c^2} - \,2{a^2}\\{c^2} = {b^2} + {a^2} - \,2{b^2}\end{array} \right. \Leftrightarrow {a^2} = {b^2} + {c^2}\)
Vậy định lí Pythagore là một trường hợp đặc biệt của định lí cosin.
Khám phá
Từ định lí cosin hãy viết các công thức tính cos A, cos B, cos C theo độ dài các cạnh a, b, c của tam giác ABC.
Phương pháp giải:
Từ định lí cosin cho tam giác ABC
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\\{b^2} = {a^2} + {c^2} - \,2a\,c.\cos B\\{c^2} = {b^2} + {a^2} - \,2ab.\cos C\end{array}\)
Rút ra công thức tính cos A, cos B, cos C.
Lời giải chi tiết:
Định lí cosin: Trong tam giác ABC
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\quad (1)\\{b^2} = {a^2} + {c^2} - \,2a\,c.\cos B\quad (2)\\{c^2} = {b^2} + {a^2} - \,2ab.\cos C\quad (3)\end{array}\)
Ta có \((1) \Leftrightarrow 2bc\cos A = {b^2} + {c^2} - {a^2}\, \Leftrightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}\,}}{{2b\,c}}.\)
Tương tự từ (2) và (3) ta suy ra \(\cos B = \frac{{{a^2} + {c^2} - {b^2}\,}}{{2a\,c}}\); \(\cos C = \frac{{{b^2} + {a^2} - {c^2}\,}}{{2b\,a}}\)
Luyện tập 1
Cho tam giác ABC có AB = 5, AC = 8 và \(\widehat A = {45^o}\). Tính độ dài các cạnh và độ lớn các góc còn lại của tam giác.
Phương pháp giải:
Bước 1: Tính cạnh BC (tương ứng là a) theo công thức \({a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\)
Bước 2: Tính cos B (theo công thức \(\cos B = \frac{{{a^2} + {c^2} - {b^2}\,}}{{2a\,c}}\)) từ đó suy ra góc B.
Bước 3: Tính góc C.
Lời giải chi tiết:
Áp dụng định lí cosin trong tam giác ABC
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\quad (1)\\{b^2} = {a^2} + {c^2} - \,2a\,c.\cos B\quad (2)\end{array}\)
(trong đó: AB = c, BC = a và AC = b)
Ta được: \(B{C^2} = {a^2} = {8^2} + {5^2} - 2.8.5.\cos {45^o} = 89 - 40\sqrt 2 \)\( \Rightarrow BC \approx 5,7\)
Từ (2) suy ra \(\cos B = \frac{{{a^2} + {c^2} - {b^2}\,}}{{2a\,c}}\);
Mà: a = BC =5,7; b =AC = 8; c =AB =5.
\( \Rightarrow \cos B \approx \frac{{ - 217}}{{1900}} \Rightarrow \widehat B \approx {97^o} \Rightarrow \widehat C \approx {38^o}\)
Vậy tam giác ABC có BC = 5,7, \(\widehat B = {97^o},\widehat C = {38^o}\)
Trải nghiệm
Vẽ một tam giác ABC, sau đó đo độ dài các cạnh, số đo góc A và kiểm tra tính đúng đắn của Định lí cosin tại đỉnh A đối với tam giác đó.
Lời giải chi tiết:
Xét tam giác ABC như hình dưới:
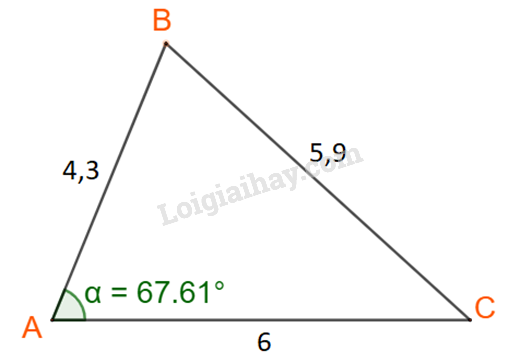
Áp dụng định lí cosin tại đỉnh A ta có:
\({a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\)
\(\begin{array}{l} \Leftrightarrow B{C^2} = {6^2} + 4,{3^2} - 2.6.4,3.\cos 67,{61^o}\\ \Leftrightarrow B{C^2} \approx 34,835\\ \Leftrightarrow BC \approx 5,9\end{array}\)
Như vậy kết quả thu được từ định lí xấp xỉ với kết quả đo được.
Nói các khác định lí cosin tại đỉnh A là đúng.
Vận dụng 1
Dùng định lí cosin, tính khoảng cách được đề cập trong HĐ 1b.
Phương pháp giải:
Khoảng cách giữa tàu và cảng Vân Phong: \(O{B^2} = O{A^2} + A{B^2} - 2.OA.AB.\cos \widehat {OAB}\)
Lời giải chi tiết:
Tàu xuất phát từ cảng Vân Phong, đi theo thướng Đông với vận tốc 20km/h. Sau khi đi 1 giờ, tàu chuyển sang hướng đông nam rồi giữ nguyên vận tốc.
Giả sử sau 1,5 giờ tàu ở vị trí điểm B.
Ta đã có: quãng đường OA = 20 (km) và quãng đường AB =10 (km)
Ngoài ra \(\widehat {OAB} = {135^o}\) (do tàu đi theo hướng đông nam)
Áp dụng định lí cosin tại đỉnh A ta được:
\(O{B^2} = O{A^2} + A{B^2} - 2.OA.AB.\cos \widehat {OAB}\)
\(\begin{array}{l} \Leftrightarrow O{B^2} = {20^2} + {10^2} - 2.20.10.\cos {135^o}\\ \Leftrightarrow O{B^2} \approx 782,84\\ \Leftrightarrow OB \approx 27,98.\end{array}\)
Vậy khoảng cách từ tàu tới cảng Vân Phong xấp xỉ 27,98 km.