HĐ1
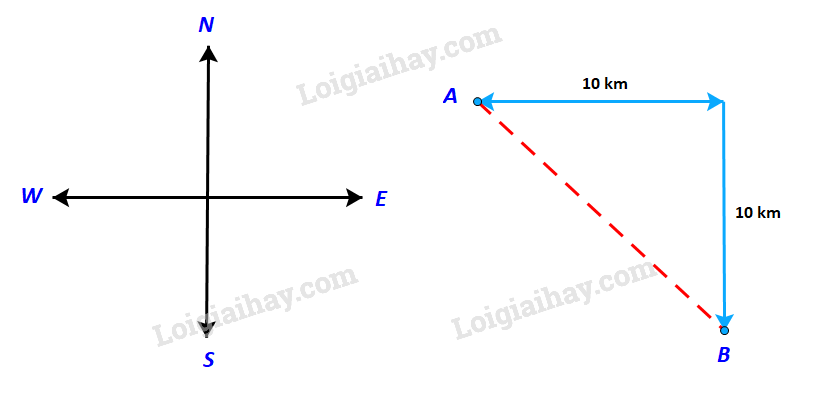
Một con tàu khởi hành từ đảo A, đi thẳng về hướng đông 10 km rồi đi thẳng tiếp về hướng nam thì tới đảo B (h.4.2). Nếu từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B, thì phải đi theo hướng nào và quãng đường phải đi dài bao nhiêu kilômét?
Phương pháp giải:
Xét tam giác, dựa vào độ dài 2 cạnh đã có để suy ra góc A.
Dựa vào định lí Pytago để tính cạnh AB
Từ đó kết luận hướng đi và quãng đường phải đi.
Lời giải chi tiết:
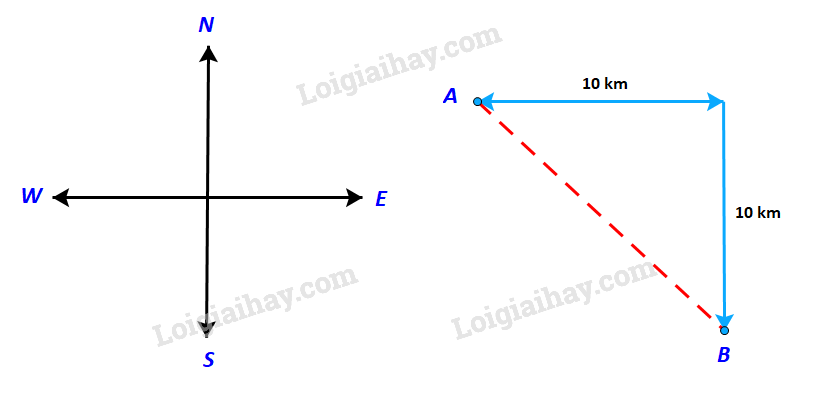
Gọi C là điểm mà tại đó tàu đổi từ hướng đông sang hướng Nam
Xét tam giác ABC ta có:
\(AC = BC = 10\;\left( {km} \right)\)
\( \Rightarrow \Delta ABC\) vuông cân tại C.
\( \Leftrightarrow \widehat A = {45^o}\)
Vậy con tàu phải đi theo hướng đông nam, góc \({45^o}\) so với hướng Đông.
Quãng đường con tàu phải đi là: \(AB = AC.\sqrt 2 = 10.\sqrt 2 \; \approx 14,142\;\left( {km} \right)\)
Luyện tập 1
Cho tam giác đều ABC với cạnh có độ dài bằng a. Hãy chỉ ra các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC.
Phương pháp giải:
Nhắc lại:
+) Vectơ là một đoạn thẳng có hướng.
+) Độ dài của vectơ là độ dài đoạn thẳng ấy.
Lời giải chi tiết:
Các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC là:
\(\overrightarrow {AB} ;\;\overrightarrow {BA} ;\;\overrightarrow {AC} ;\;\overrightarrow {CA} ;\;\overrightarrow {BC} ;\;\overrightarrow {CB} \)
Chú ý khi giải:
Vectơ \(\overrightarrow {AB} \) khác vectơ \(\overrightarrow {BA} \) (khác nhau điểm đầu và điểm cuối).

