Đề bài
Cho hình vuông ABCD có cạnh a. Khẳng định nào sau đây là đúng?
A. \(\left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = {45^o}\)
B. \(\left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = {45^o}\) và \(\overrightarrow {AC} .\overrightarrow {BC} = {a^2}\)
C. \(\overrightarrow {AC} .\overrightarrow {BD} = {a^2}\sqrt 2 \)
D. \(\overrightarrow {BA} .\overrightarrow {BD} = - {a^2}\)
Phương pháp giải - Xem chi tiết
Tính tích vô hướng bằng công thức: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\,\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
Lời giải chi tiết
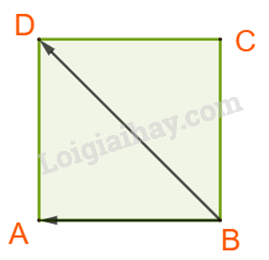
A. Ta có: \(\left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = \left( {\overrightarrow {BE} ,\overrightarrow {BD} } \right) = {135^o} \ne {45^o}.\) Vậy A sai.
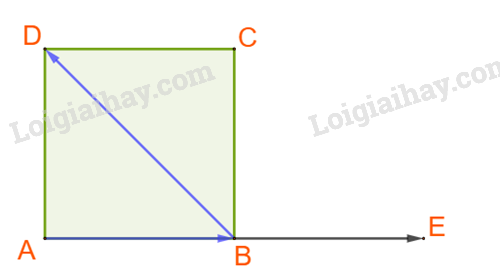
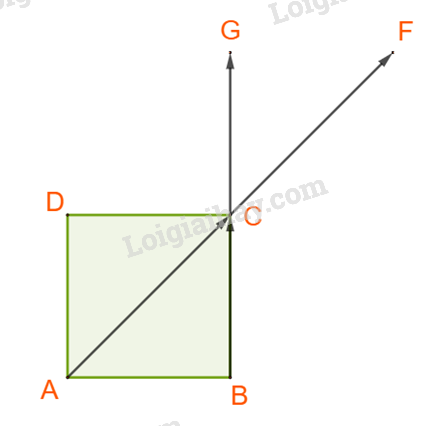
B. Ta có: \(\left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {CF} ,\overrightarrow {CG} } \right) = {45^o}\) và \(\overrightarrow {AC} .\overrightarrow {BC} = AC.BC.\cos {45^o} = a\sqrt 2 .a.\frac{{\sqrt 2 }}{2} = {a^2}.\)
Vậy B đúng.
Chọn B
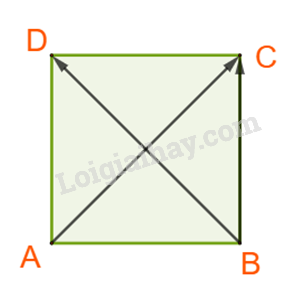
C. Dễ thấy \(AC \bot BD\) nên \(\overrightarrow {AC} .\overrightarrow {BD} = 0 \ne {a^2}\sqrt 2.\) Vậy C sai.
D. Ta có: \(\left( {\overrightarrow {BA} .\overrightarrow {BD} } \right) = {45^o}\) \( \Rightarrow \overrightarrow {BA} .\overrightarrow {BD} = BA.BD.\cos {45^o} = a.a\sqrt 2 .\frac{{\sqrt 2 }}{2} = {a^2} \ne - {a^2}.\) Vậy D sai.