HĐ2
Nêu nhận xét về vị trí của hai điểm M, M’ đối với trục Oy. Từ đó nêu các mối quan hệ giữa \(\sin \alpha \) và \(\sin \left( {{{180}^o} - \alpha } \right)\), giữa \(\cos \alpha \) và \(\cos \left( {{{180}^o} - \alpha } \right)\).
Phương pháp giải:
Nhận xét vị trí của M và M’ trong mỗi trường hợp: \(\alpha = {90^o};\;\alpha < {90^o};\;\alpha > {90^o}.\)
Khi \({0^o} < \alpha < {90^o}\): \(\cos \alpha ,\;\sin \alpha \) tương ứng là hoành độ và tung độ của điểm M.
Lời giải chi tiết:
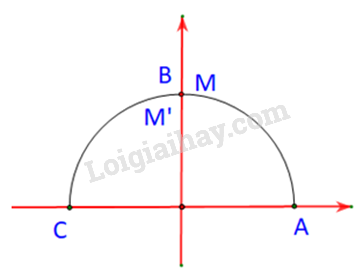
M, M’ là hai điểm trên nửa đường tròn đơn vị tương ứng với hai góc \(\alpha \) và \({180^o} - \alpha \).
Giả sử \(M\left( {{x_0};{y_o}} \right)\). Khi đó \(\cos \alpha = {x_0};\;\;\sin \alpha = {y_o}\)
Trường hợp 1: \(\alpha = {90^o}\)
Khi đó \(\alpha = {180^o} - \alpha = {90^o}\)
Tức là M và M’ lần lượt trùng nhau và trùng với B.
Và \(\left\{ \begin{array}{l}\cos \alpha = - \cos \left( {{{180}^o} - \alpha } \right) = 0;\\\sin \alpha = \sin \left( {{{180}^o} - \alpha } \right) = \sin {90^o} = 1.\\\cot \alpha = 0\end{array} \right.\)
Không tồn tại \(\tan \alpha \) với \(\alpha = {90^o}\)
Trường hợp 2: \(\alpha < {90^o} \Rightarrow {180^o} - \alpha > {90^o}\)
M nằm bên phải trục tung
M’ nằm bên trái trục tung
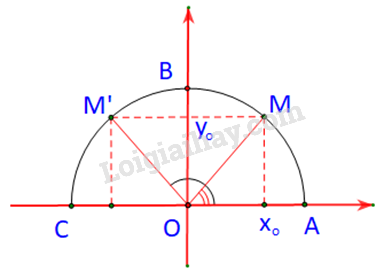
Dễ thấy: \(\widehat {M'OC} = {180^o} - \widehat {xOM'} = {180^o} - \left( {{{180}^o} - \alpha } \right) = \alpha = \widehat {xOM}\)
\( \Rightarrow \widehat {M'OB} = {90^o} - \widehat {M'OC} = {90^o} - \widehat {MOA} = \widehat {MOB}\)
Xét tam giác \(M'OB\) và tam giác \(MOB\) ta có:
\(OM = OM'\)
\(\widehat {M'OB} = \widehat {MOB}\)
OB chung
\(\begin{array}{l} \Rightarrow \Delta MOB = \Delta M'OB\\ \Rightarrow \left\{ \begin{array}{l}OM = OM'\\BM = BM'\end{array} \right.\end{array}\)
Hay OB là trung trực của đoạn thẳng MM’.
Nói cách khác M và M’ đối xứng với nhau qua trục tung.
Mà \(M\left( {{x_0};{y_o}} \right)\) nên \(M'\left( { - {x_0};{y_o}} \right)\)
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - {x_0} = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = {y_o} = \sin \alpha .\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array} \right.\end{array}\)
Trường hợp 3: \(\alpha > {90^o} \Rightarrow {180^o} - \alpha < {90^o}\)
Khi đó M nằm bên trái trục tung và M’ nằm bên phải trục tung.
Tương tự ta cũng chứng minh được M và M’ đối xứng với nhau qua trục tung.
Như vậy
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - {x_0} = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = {y_o} = \sin \alpha .\\ \Rightarrow \left\{ \begin{array}{l}\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array} \right.\end{array}\)
Kết luận: Với mọi \({0^o} < \alpha < {180^o}\), ta luôn có
\(\begin{array}{l}\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha ;\\\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha .\\\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha \;\;\;(\alpha \ne {90^o})\\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha \end{array}\)
Luyện tập 2
Trong Hình 3.6, hai điểm M, N ứng với hai góc phụ nhau \(\alpha \) và \({90^o} - \alpha \) (\(\widehat {xOM} = \alpha ,\;\;\widehat {xON} = {90^o} - \alpha \)). Chứng mình rằng \(\Delta MOP = \Delta NOQ\). Từ đó nêu mối quan hệ giữa \(\cos \alpha \) và \(\sin \left( {{{90}^o} - \alpha } \right)\).
Phương pháp giải:
Nhận xét vị trí của M và N trong mỗi trường hợp: \(\alpha = {90^o};\;\alpha < {90^o}\)
Khi \({0^o} < \alpha < {90^o}\): \(\cos \alpha ,\;\sin \alpha \) tương ứng là hoành độ và tung độ của điểm M.
Lời giải chi tiết:
Trường hợp 1: \(\alpha = {90^o}\)
Khi đó \({90^o} - \alpha = {0^o}\)
Tức là M và N lần lượt trùng nhau với B và A.
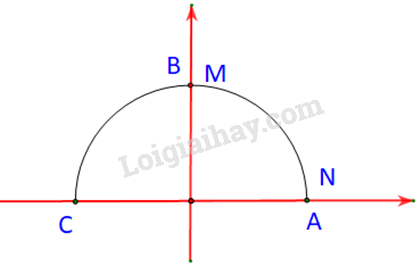
Và \(\cos \alpha = 0 = \sin \left( {{{90}^o} - \alpha } \right)\)
Trường hợp 2: \({0^o} < \alpha < {90^o} \Rightarrow {0^o} < {90^o} - \alpha < {90^0}\)
M và N cùng nằm bên trái phải trục tung.
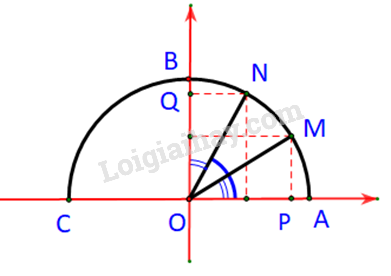
Ta có: \(\alpha = \widehat {AOM};\;\;{90^o} - \alpha = \widehat {AON}\)
Dễ thấy: \(\widehat {AON} = {90^o} - \alpha = {90^o} - \widehat {NOB}\;\;\; \Rightarrow \alpha = \widehat {NOB}\)
Xét hai tam giác vuông \(NOQ\) và tam giác \(MOP\) ta có:
\(OM = ON\)
\(\widehat {POM} = \widehat {QON}\)
\(\begin{array}{l} \Rightarrow \Delta NOQ = \Delta MOP\\ \Rightarrow \left\{ \begin{array}{l}OP = OQ\\QN = MP\end{array} \right.\end{array}\)
Mà \(M\left( {{x_0};{y_o}} \right)\) nên \(N\left( {{y_o};{x_0}} \right)\). Nói cách khác:
\(\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha ;\;\;\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha .\)
Vận dụng
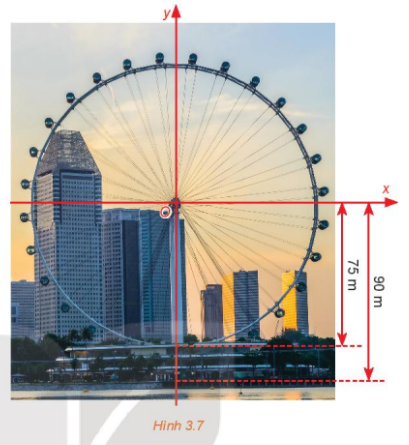
Một chiếc đu quay có bán kính 75 m, tâm của vòng quay ở độ cao 90 m (H.3.7), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét?
Phương pháp giải:
Bước 1: Giả sử chiều quay của chiếc đu quay. Xác định vị trí của cabin sau 20 phút.
Bước 2: Dựa vào giá trị lượng giác của góc, xác định khoảng cách từ cabin đến Ox (trong hình H.3.7)
Bước 3: Suy ra độ cao của người đó sau 20 phút quay.
Lời giải chi tiết:
Giả sử chiếc đu quay quay theo chiều kim đồng hồ.
Gọi M là vị trí của cabin, M’ là vị trí của cabin sau 20 phút và các điểm A A’, B, H như hình dưới.
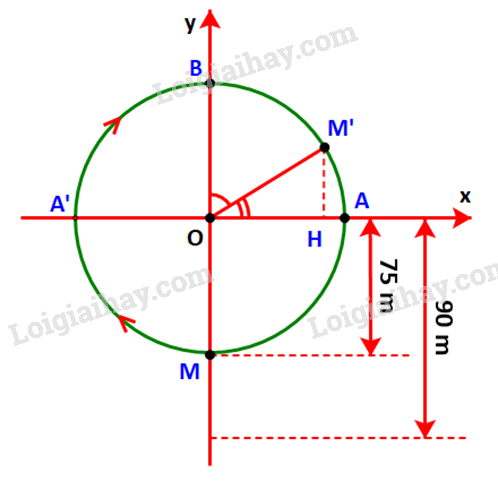
Vì đi cả vòng quay mất 30 phút nên sau 20 phút, cabin sẽ đi quãng đường bằng \(\frac{2}{3}\) chu vi đường tròn.
Sau 15 phút cabin đi chuyển từ điểm M đến điểm B, đi được \(\frac{1}{2}\) chu vi đường tròn.
Trong 5 phút tiếp theo cabin đi chuyển từ điểm B đến điểm M’ tương ứng \(\frac{1}{6}\) chu vi đường tròn hay \(\frac{1}{3}\) cung .
Do đó: \(\widehat {BOM'} = \frac{1}{3}{.180^o} = {60^o}\)\( \Rightarrow \widehat {AOM'} = {90^o} - {60^o} = {30^o}.\)
\( \Rightarrow M'H = \sin {30^o}.OM' = \frac{1}{2}.75 = 37,5\left( m \right).\)
\( \Rightarrow \) Độ cao của người đó là: 37,5 + 90 = 127,5 (m).
Vậy sau 20 phút quay người đó ở độ cao 127,5 m.

