Bài tập thời gian nén - giãn của con lắc lò xo

+ Biên độ dao động: $A = 10cm$

+ Độ dãn của lò xo tại VTCB: $\Delta l = \dfrac{{mg}}{k} = \dfrac{{0,4.10}}{{80}} = 0,05m = 5cm$

Chu kì dao động: $T = 2\pi \sqrt {\dfrac{m}{k}}  = 2\pi \sqrt {\dfrac{{0,4}}{{80}}}  = \dfrac{{\sqrt 5 }}{5} \approx {\rm{0}}{\rm{,45s}}$

Chọn chiều dương hướng xuống:

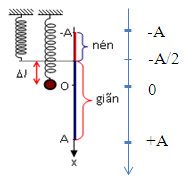
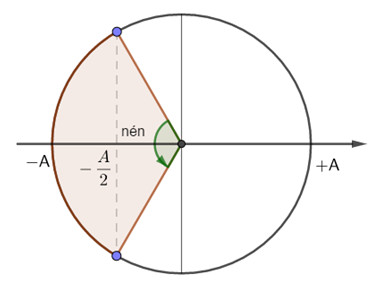
=> Thời gian nén của lò xo trong một chu kì là: ${t_{nen}} = 2\dfrac{T}{6} = \dfrac{T}{3} = \dfrac{{0,45}}{3} = 0,15s$

Ta có:

- Biên độ $A = 3cm$

- Độ dãn tại VTCB của lò xo: $\Delta l = \dfrac{{mg\sin \alpha }}{k} = \dfrac{{120.10^{-3}.10\sin {{45}^0}}}{{16}} = 0,053m = 5,3cm > A$

=> Lò xo luôn luôn dãn

=> Thời gian lò xo nén bằng 0

Ta có:  

+ Độ dãn của lò xo ở VTCB: $\Delta l = \dfrac{{mg}}{k} = \dfrac{{1,2.10}}{{160}} = 0,075m = 7,5cm$

Chu kỳ dao động của con lắc: $T = 2\pi \sqrt {\dfrac{m}{k}}  = 2\pi \sqrt {\dfrac{{1,2}}{{160}}}  \approx 0,55{\rm{s}}$

$\dfrac{{{t_n}}}{T} = \dfrac{{0,14}}{{0,55}} \approx 0,25 \to {t_n} = 0,25T = \dfrac{T}{4}$

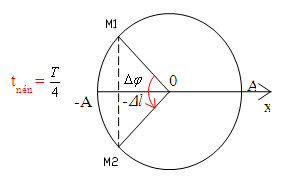
Ta có: $\Delta \varphi  = \omega \Delta t = \dfrac{{2\pi }}{T}.\dfrac{T}{4} = \dfrac{\pi }{2}$

$\begin{array}{l} \to \Delta l = Acos\dfrac{{\Delta \varphi }}{2} = Acos\dfrac{\pi }{4} = \dfrac{A}{{\sqrt 2 }}\\ \to A = \sqrt 2 \Delta l = 7,5\sqrt 2 cm\end{array}$

Ta có:  

+ Độ dãn của lò xo ở VTCB: $\Delta l = \dfrac{{mg}}{k} = \dfrac{{0,25.10}}{{160}} = 0,015625m = 1,5625cm = \left| {\dfrac{A}{2}} \right|$

+ Chu kỳ dao động của con lắc: $T = 2\pi \sqrt {\dfrac{m}{k}}  = 2\pi \sqrt {\dfrac{{0,25}}{{160}}}  = 0,25{\rm{s}}$

Chọn chiều dương hướng xuống:

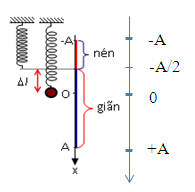
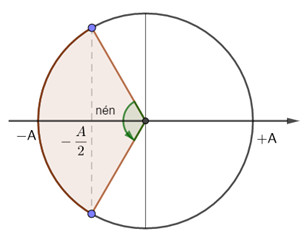
 $\Delta l =  - \dfrac{A}{2} \to \left\{ \begin{array}{l}{t_n} = \Delta {t_1} = 2{t_{( - A \to \dfrac{{ - A}}{2})}} = 2.\dfrac{T}{6} = \dfrac{T}{3} = \dfrac{1}{{12}}s\\{t_g} = \Delta {t_2} = T - {t_n} = \dfrac{{2T}}{3} = \dfrac{1}{6}s\end{array} \right.$

+ Độ dãn của lò xo ở VTCB: $\Delta l = 4cm$

+ Chu kỳ dao động của con lắc: $T = 2\pi \sqrt {\dfrac{{\Delta l}}{g}}  = 2\pi \sqrt {\dfrac{{0,04}}{{10}}}  = 0,4{\rm{s}}$

$\dfrac{{{t_n}}}{T} = \dfrac{{\dfrac{1}{{15}}}}{{0,4}} = \dfrac{1}{6} \to {t_n} = \dfrac{T}{6}$

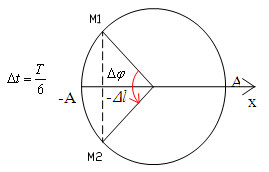
Ta có: $\Delta \varphi  = \omega \Delta t = \dfrac{{2\pi }}{T}.\dfrac{T}{6} = \dfrac{\pi }{3}$

$\begin{array}{l} \to \Delta l = Acos\dfrac{{\Delta \varphi }}{2} = Acos\dfrac{\pi }{6} = \dfrac{{A\sqrt 3 }}{2}\\ \to A = \dfrac{{2\Delta l}}{{\sqrt 3 }} = \dfrac{{2.4}}{{\sqrt 3 }} = \dfrac{8}{{\sqrt 3 }}cm\end{array}$

+ Độ dãn của lò xo ở VTCB: $\Delta l = \dfrac{{mg}}{k} = \dfrac{{0,32.10}}{{80}} = 0,04m = 4cm$

+ Chu kỳ dao động của con lắc: $T = 2\pi \sqrt {\dfrac{m}{k}}  = 2\pi \sqrt {\dfrac{{0,32}}{{80}}}  = \dfrac{2}{5}s$

Ta có:

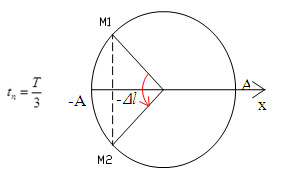
$\left\{ \begin{array}{l}{t_{nen}} = 2{t_{\left( { - A \to  - \dfrac{A}{2}} \right)}} = 2.\dfrac{T}{6} = \dfrac{T}{3}\\{t_{gian}} = T - {t_{nen}} = T - \dfrac{T}{3} = \dfrac{{2T}}{3} = \dfrac{2}{3}\dfrac{2}{5} = \dfrac{4}{{15}}s\end{array} \right.$

- Khi chỉ có ${m_1}$ thì lò xo dãn 1 đoạn: $\Delta {l_0} = \dfrac{{{m_1}g}}{k} = 5cm$

- Khi treo đồng thời ${m_1}$ và ${m_2}$ thì lò xo dãn 1 đoạn: $\Delta l = \dfrac{{\left( {{m_1} + {m_2}} \right)g}}{k} = \dfrac{{3{m_1}g}}{k} = 3.\Delta {l_0} = 15cm$

- Khi dây đứt, vật ${m_1}$ đang có vận tốc bằng 0 (đang ở vị trí biên)

Ngay sau khi đứt dây, ${m_1}$ dao động điều hòa quanh VTCB chính là vị trí mà lò xo dãn $5cm$ với biên độ:

$A = \Delta l - \Delta {l_0} = 15 - 5 = 10cm$

Chu kỳ dao động của con lắc: $T = 2\pi \sqrt {\dfrac{{\Delta {l_0}}}{g}}  = 2\pi \sqrt {\dfrac{{0,05}}{{10}}}  = \dfrac{{\pi \sqrt 2 }}{{10}}s$

Ta có:

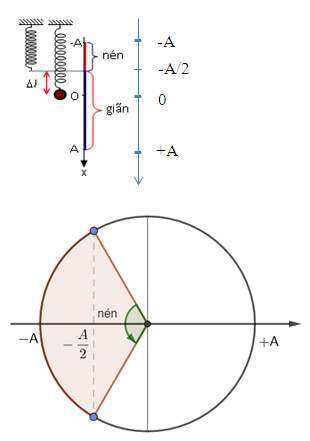
${t_{nen}} = 2{t_{\left( { - A \to  - \dfrac{A}{2}} \right)}} = 2.\dfrac{T}{6} = \dfrac{T}{3} = \dfrac{{\pi \sqrt 2 }}{{30}} \approx 0,148{\rm{s}}$

- Độ dãn của lò xo tại VTCB: $\Delta l = \dfrac{{mg}}{k} = \dfrac{{0,5.10}}{{80}} = 0,0625m = 6,25cm$

Biên độ dao động: $A = 10cm$

- Tần số góc: $\omega  = \sqrt {\dfrac{k}{m}}  = \sqrt {\dfrac{{80}}{{0,5}}}  = 4\sqrt {10}  = 4\pi ({\rm{r}}a{\rm{d}}/s)$

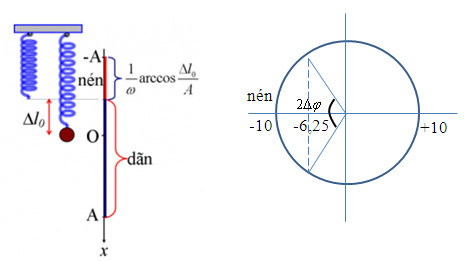
${\rm{cos}}\Delta \varphi  = \dfrac{{6,25}}{{10}} = \dfrac{5}{8} \to \Delta \varphi  = {\rm{ar}}cc{\rm{os}}\dfrac{5}{8} \approx 0,285\pi$

=> Trong 1 chu kì, thời gian lò xo nén là: ${t_{nen}} = \dfrac{{2\Delta \varphi }}{\omega } = \dfrac{2}{\omega }{\rm{ar}}cc{\rm{os}}\dfrac{5}{8} = \dfrac{2}{{4\pi }}{\rm{ar}}cc{\rm{os}}\dfrac{5}{8} = 0,143{\rm{s}}$

Ta có:

- Chiều dài quỹ đạo $L = 2A = 30cm \to A = 15cm$

- Trong 1 nửa chu kì, tỉ số giữa thời gian lò xo giãn và thời gian lò xo nén là: $\dfrac{{{t_{gian}}}}{{{t_{nen}}}} = \dfrac{{\dfrac{T}{2} - {t_{nen}}}}{{{t_{nen}}}} = 2 \to {t_{nen}} = \dfrac{T}{6}$

Chọn chiều dương hướng xuống, ta có:

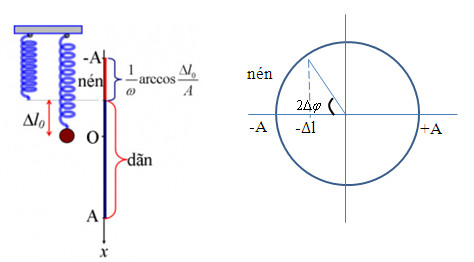
$\begin{array}{l}\Delta \varphi  = \omega .\Delta t = \dfrac{{2\pi }}{T}.\dfrac{T}{6} = \dfrac{\pi }{3}\\ \to \Delta l = Ac{\rm{os}}\dfrac{\pi }{3} = \dfrac{A}{2} = 7,5cm\end{array}$

Mặt khác, ta có: $\Delta l = \dfrac{{mg}}{k} = \dfrac{g}{{{\omega ^2}}} = \dfrac{g}{{4{\pi ^2}}}{T^2} = 0,075 \to T = \sqrt {\dfrac{{0,075.4{\pi ^2}}}{{10}}}  = 0,544{\rm{s}}$

Thế năng của con lắc biến thiên với chu kì: $T' = \dfrac{T}{2} = \dfrac{{0,544}}{2} = 0,272s$

Chọn chiều dương hướng xuống

Ta có:

+ Thời điểm ban đầu: ${x_0} =  + A \to \left| a \right| = \left| {{a_{max}}} \right| = {\omega ^2}A$

Vị trí gia tốc của vật bằng nửa gia tốc ban đầu: ${a_2} = {\rm{ }}0,5a$

Mà gia tốc tỉ lệ với li độ: $a{\rm{ }} = {\rm{ }} - {\omega ^2}x$

=> Li độ tại vị trí gia tốc của vật bằng nửa gia tốc ban đầu: $x = \dfrac{A}{2}$

+ Theo đề bài, ta có: thời gian vật đi từ $A \to \dfrac{A}{2}$ là: $t = 0,05s = \dfrac{T}{6} \to T = 0,3s$

+ Độ dãn của lò xo tại VTCB: $\Delta l = \dfrac{{mg}}{k} = \dfrac{g}{{{\omega ^2}}} = \dfrac{g}{{4{\pi ^2}}}{T^2} = \dfrac{{10}}{{4{\pi ^2}}}{\left( {0,3} \right)^2} = 0,0225m = 2,25cm$

=> Biên độ: $A = 6,75 - \Delta l = 6,75 - 2,25 = 4,5cm$

$\to \left| {\Delta l} \right| = 2,25cm = \dfrac{A}{2}$

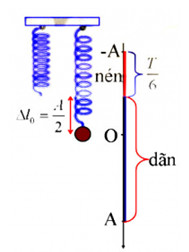
=> Thời gian lò xo bị nén trong 1 chu kì:  $t = 2\dfrac{T}{6} = \dfrac{T}{3} = \dfrac{{0,3}}{3} = 0,1s$

Ta có:

+ Tần số góc của dao động: $\omega  = \sqrt {\dfrac{k}{m}}  = \sqrt {\dfrac{{120}}{{0,3}}}  = 20(ra{\rm{d}}/s)$

+ Biên độ dao động: ${A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {3^2} + {\left( {\dfrac{{80}}{{20}}} \right)^2} \to A = 5cm$

+ Độ dãn của lò xo tại VTCB: $\Delta l = \dfrac{{mg}}{k} = \dfrac{{0,3.10}}{{120}} = 0,025 = 2,5cm$

Chọn chiều dương hướng xuống, ta có:

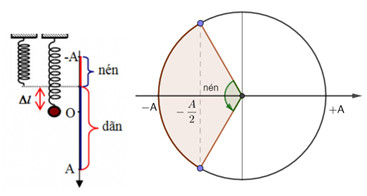
=> Thời gian lò xo bị nén trong 1 chu kì là: $t = 2\dfrac{T}{6} = \dfrac{T}{3} = \dfrac{{\dfrac{{2\pi }}{\omega }}}{3} = \dfrac{{2\pi }}{{20.3}} = \dfrac{\pi }{{30}}s$

Ta có:

+ Độ cứng của con lắc lò xo: ${\rm{?}}$

+ Độ dãn của lò xo tại VTCB: $\Delta l = \dfrac{{mg}}{k} = \dfrac{{0,1.10}}{{10}} = 0,1m = 10cm > A = 8cm$

=> Lò xo luôn dãn

Khi lực đàn hồi bằng 1,3N thì lò xo dãn 1 đoạn ∆x: $\left| {{F_{dh}}} \right| = k\Delta x \to \Delta x = \dfrac{{\left| {{F_{dh}}} \right|}}{k} = \dfrac{{1,2}}{{10}} = 0,12m = 12cm$

=> Li độ của vật khi đó: $x = \Delta x - A= 12 - 8 = 4cm$

=> Bài toán tương đương với việc tìm thời gian trong một chu kì vật có li độ $x \ge 4cm$

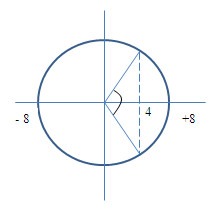
Từ vòng tròn lượng giác,

Ta có: $\Delta \varphi  = \dfrac{{2\pi }}{3}$

Mặt khác, ta có: $\Delta \varphi  = \omega \Delta t$

=> Trong 1 chu kì, thời gian vật có li độ $x \ge 4cm$ là: $\Delta t = \dfrac{{\Delta \varphi }}{\omega } = \dfrac{{\dfrac{{2\pi }}{3}}}{{\dfrac{{2\pi }}{T}}} = \dfrac{T}{3} = \dfrac{{0,2\pi}}{3} = \dfrac{\pi}{{15}}s$

Ta có:

+ Độ dãn của lò xo tại VTCB: $\Delta l = \dfrac{{mg}}{k} = \dfrac{g}{{{\omega ^2}}} = \dfrac{g}{{4{\pi ^2}}}{T^2} = \dfrac{{10}}{{4{\pi ^2}}}.{(0,6)^2} = 0,09m = 9cm$

+ Biên độ $A = 6\sqrt 3 cm$

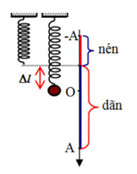
+ Vị trí lực đàn hồi của lò xo có độ lớn cực tiểu là: $x =  - \Delta l =  - 9cm =  - \dfrac{{A\sqrt 3 }}{2}$

Tại t = 0: $\left\{ \begin{array}{l}x = 0\\v > 0\end{array} \right.$

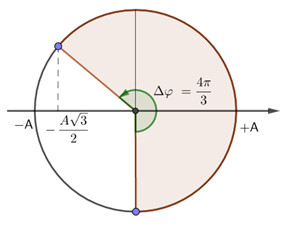
=> Thời gian ngắn nhất kể từ t = 0 đến khi lực đàn hồi của lò xo có độ lớn cực tiểu là thời gian vật đi từ $0 \to A \to 0 \to  - \dfrac{A}{2}$

Ta có: $\Delta \varphi  = \dfrac{{4\pi }}{3} = \omega \Delta t$

: $\to \Delta t = \dfrac{{\Delta \varphi }}{\omega } = \dfrac{{\dfrac{{4\pi }}{3}}}{{\dfrac{{2\pi }}{T}}} = \dfrac{{2T}}{3} = \dfrac{{2.0,6}}{3} = 0,4s$

Chu kì dao động của vật: $T = 2\pi \sqrt {\dfrac{m}{k}}  = 2\pi \sqrt {\dfrac{{0,3}}{{120}}}  = 0,1\pi {\rm{s}}$

Tần số góc: $\omega  = \dfrac{{2\pi }}{T} = 20({\rm{r}}a{\rm{d}}/s)$

Biên độ dao động: $A = \sqrt {{x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}}  = \sqrt {{{\left( {2,5\sqrt 2 } \right)}^2} + \dfrac{{{{(50\sqrt 2 )}^2}}}{{{{(20)}^2}}}}  = 5cm$

Độ dãn của lò xo tại VTCB: $\Delta l = \dfrac{{mg}}{k} = \dfrac{{0,3.10}}{{120}} = 0,025m = 2,5cm$

=> Vị trí lò xo dãn $2,5cm$ là $x =  + \dfrac{A}{2}$

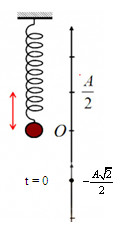
Thời gian từ lúc bắt đầu dao động đến lúc vật qua vị trí mà lò xo dãn $2,5cm$ lần đầu tiên (khoảng thời gian vật đi từ $- \dfrac{{A\sqrt 2 }}{2} \to \dfrac{A}{2}$) là:

$t = \dfrac{T}{8} + \dfrac{T}{{12}} = \dfrac{{5T}}{{24}} = \dfrac{5}{{24}}.0,1\pi  = \dfrac{\pi }{{48}}s$

Ta có: $\Delta l = \dfrac{{mg}}{k} = \dfrac{g}{{{\omega ^2}}} = \dfrac{g}{{4{\pi ^2}}}{T^2} = 0,04 \to T = \sqrt {\dfrac{{4{\pi ^2}.0,04}}{{10}}}  = 0,4{\rm{s}}$

Biên độ dao động: $A{\rm{ }} = {\rm{ }}8cm$

Chọn chiều dương hướng lên, ta có:

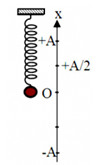
- Lò xo không biến dạng khi $x = \dfrac{A}{2}$

Thời điểm thứ $2019$ lò xo có chiều dài tự nhiên: ${t_{2019}} = {t_{2018}} + {t_1}$

+ Trong 1 chu kì vật qua vị trí có chiều dài tự nhiên 2 lần ${t_{2018}} = \dfrac{{2018}}{2}T = 1009T$

+ Tại t = 0, vật đang ở biên +A

=> Thời điểm ban đầu vật qua vị trí có chiều dài tự nhiên (thời gian từ $A \to \dfrac{A}{2}$): ${t_1} = \dfrac{T}{6}$

=> Thời điểm thứ $2019$ lò xo có chiều dài tự nhiên: $t = {t_{2018}} + {t_1} = 1009T + \dfrac{T}{6} = \dfrac{{6055T}}{6} \approx 403,67{\rm{s}}$

+ Tần số góc của dao động:

$\omega  = \sqrt {\dfrac{k}{m}}  = \sqrt {\dfrac{{100}}{{0,1}}}  = 10\pi ra{\rm{d}}/s$

+ Độ dãn của lò xo tại vị trí cân bằng:

$\Delta l = \dfrac{{mg}}{k} = \dfrac{{0,1.10}}{{100}} = 0,01m = 1cm$

Chọn chiều dương hướng xuống.

Kéo vật đến vị trí lò xo dãn 4cm $\Rightarrow$ tại đó có: $\left\{ \begin{array}{l}x = 3cm\\v = 40\pi cm/s\end{array} \right.$

Áp dụng CT độc lập ta có:

${A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} \Rightarrow A = \sqrt {{3^2} + {{\left( {\dfrac{{40\pi }}{{10\pi }}} \right)}^2}}  = 5cm$

Vị trí thấp nhất là biên dưới: $x = A$

Vị trí lò xo bị nén 1,5cm ứng với li độ: $x =  - 2,5cm$

Vẽ trên vòng tròn lượng giác ta được:

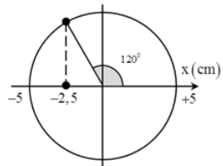
Từ vòng tròn lượng giác ta suy ra, thời gian ngắn nhất để vật chuyển động từ vị trí thấp nhất đến vị trí lò xo nén 1,5cm là:

$t = \dfrac{T}{4} + \dfrac{T}{{12}} = \dfrac{T}{3} = \dfrac{{\dfrac{{2\pi }}{{10\pi }}}}{3} = \dfrac{1}{{15}}s$

Biên độ dao động: A = 50cm

Độ dãn của lò xo tại VTCB: $\Delta l = \frac{{mg}}{k} = \frac{{0,25.10}}{{10}} = 0,25m = 25cm$

Chu kì dao động: $T = 2\pi \sqrt {\frac{m}{k}}  = 2\pi \sqrt {\frac{{0,25}}{{10}}}  = 1{\rm{s}}$

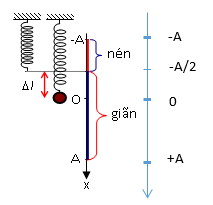
Chọn chiều dương hướng xuống:

=> Thời gian nén của lò xo trong một chu kì là: ${t_{nen}} = 2\frac{T}{6} = \frac{T}{3} = \frac{1}{3}s$

- Biên độ A = 4cm

- Độ dãn tại VTCB của lò xo: $\Delta l = \frac{{mg\sin \alpha }}{k} = \frac{{1.10\sin 30}}{{100}} = 0,05m = 5cm > A$

=> Lò xo luôn luôn dãn

=> Thời gian lò xo nén bằng 0

Ta có:  

Độ dãn của lò xo ở VTCB: $\Delta l = \dfrac{{mg}}{k} = \dfrac{{0,4.10}}{{100}} = 0,04m = 4cm$

Chu kỳ dao động của con lắc: $T = 2\pi \sqrt {\dfrac{m}{k}}  = 2\pi \sqrt {\dfrac{{0,4}}{{100}}}  = 0,4{\rm{s}}$

$\dfrac{{{t_n}}}{T} = \dfrac{{0,1}}{{0,4}} = \dfrac{1}{4} \to {t_n} = \dfrac{T}{4}$

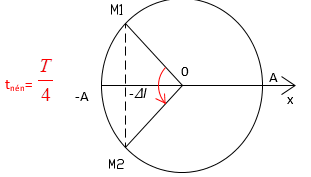
=> $\Delta l = \dfrac{A}{{\sqrt 2 }} \to A = \sqrt 2 \Delta l = 4\sqrt 2 cm$

Ta có:  

Độ dãn của lò xo ở VTCB: $\Delta l = \frac{{mg}}{k} = 0,05m = 5cm = \frac{A}{2}$

Chu kỳ dao động của con lắc: $T = 2\pi \sqrt {\frac{m}{k}}  = 2\pi \sqrt {\frac{{0,5}}{{100}}}  = \frac{\pi }{{5\sqrt 2 }}{\rm{s}}$

 $\Delta l = \frac{A}{2} \to \left\{ \begin{array}{l}{t_n} = \Delta {t_1} = 2{t_{( - A \to \frac{{ - A}}{2})}} = 2.\frac{T}{6} = \frac{T}{3} = \frac{\pi }{{15\sqrt 2 }}s\\{t_g} = \Delta {t_2} = T - {t_n} = \frac{{2T}}{3} = \frac{{2\pi }}{{15\sqrt 2 }}s\end{array} \right.$