Con lắc lò xo thẳng đứng gồm lò xo nhẹ đầu trên cố định, đầu dưới treo vật nặng m1, khi vật nằm cân bằng lò xo dãn \(5cm\). Vật \({m_2} = 2{m_1}\) được nối với \({m_1}\) bằng một dây mềm, nhẹ. Khi hệ thống cân bằng, đốt dây nối để \({m_1}\) dao động điều hòa, lấy \(g{\rm{ }} = {\rm{ }}10m/{s^2}\). Trong 1 chu kỳ dao động của \({m_1}\) thời gian lò xo bị nén là:
Trả lời bởi giáo viên
- Khi chỉ có \({m_1}\) thì lò xo dãn 1 đoạn: \(\Delta {l_0} = \dfrac{{{m_1}g}}{k} = 5cm\)
- Khi treo đồng thời \({m_1}\) và \({m_2}\) thì lò xo dãn 1 đoạn: \(\Delta l = \dfrac{{\left( {{m_1} + {m_2}} \right)g}}{k} = \dfrac{{3{m_1}g}}{k} = 3.\Delta {l_0} = 15cm\)
- Khi dây đứt, vật \({m_1}\) đang có vận tốc bằng 0 (đang ở vị trí biên)
Ngay sau khi đứt dây, \({m_1}\) dao động điều hòa quanh VTCB chính là vị trí mà lò xo dãn \(5cm\) với biên độ:
\(A = \Delta l - \Delta {l_0} = 15 - 5 = 10cm\)
Chu kỳ dao động của con lắc: \(T = 2\pi \sqrt {\dfrac{{\Delta {l_0}}}{g}} = 2\pi \sqrt {\dfrac{{0,05}}{{10}}} = \dfrac{{\pi \sqrt 2 }}{{10}}s\)
Ta có:
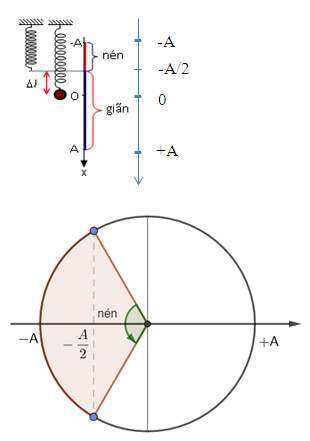
\({t_{nen}} = 2{t_{\left( { - A \to - \dfrac{A}{2}} \right)}} = 2.\dfrac{T}{6} = \dfrac{T}{3} = \dfrac{{\pi \sqrt 2 }}{{30}} \approx 0,148{\rm{s}}\)
Hướng dẫn giải:
+ Vận dụng biểu thức xác định độ dãn tại vị trí cân bằng của con lắc lò xo treo thẳng đứng: \(\Delta l = \dfrac{{mg}}{k}\)
+ Sử dụng công thức tính chu kỳ dao động của con lắc: \(T = 2\pi \sqrt {\dfrac{{\Delta l}}{g}} \)
+ Xác định vị trí lò xo bị nén => thời gian nén

