Một con lắc lò xo dao động điều hòa theo phương thẳng đứng, khi con lắc ở vị trí cân bằng lò xo giãn \(4cm\), thời gian lò xo bị nén trong 1 chu kỳ là \(\dfrac{1}{{15}}s\), lấy \(g{\rm{ }} = {\pi ^2} = 10{\rm{ }}m/{s^2}\). Biên độ dao động của vật là:
Trả lời bởi giáo viên
+ Độ dãn của lò xo ở VTCB: \(\Delta l = 4cm\)
+ Chu kỳ dao động của con lắc: \(T = 2\pi \sqrt {\dfrac{{\Delta l}}{g}} = 2\pi \sqrt {\dfrac{{0,04}}{{10}}} = 0,4{\rm{s}}\)
\(\dfrac{{{t_n}}}{T} = \dfrac{{\dfrac{1}{{15}}}}{{0,4}} = \dfrac{1}{6} \to {t_n} = \dfrac{T}{6}\)
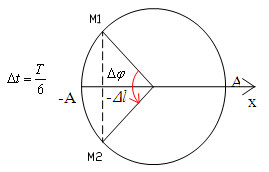
Ta có: \(\Delta \varphi = \omega \Delta t = \dfrac{{2\pi }}{T}.\dfrac{T}{6} = \dfrac{\pi }{3}\)
\(\begin{array}{l} \to \Delta l = Acos\dfrac{{\Delta \varphi }}{2} = Acos\dfrac{\pi }{6} = \dfrac{{A\sqrt 3 }}{2}\\ \to A = \dfrac{{2\Delta l}}{{\sqrt 3 }} = \dfrac{{2.4}}{{\sqrt 3 }} = \dfrac{8}{{\sqrt 3 }}cm\end{array}\)
Hướng dẫn giải:
+ Xác định độ dãn của lò xo ở VTCB: \(\Delta l = \dfrac{{mg}}{k}\)
+ Sử dụng công thức tính chu kỳ dao động của con lắc: \(T = 2\pi \sqrt {\dfrac{{\Delta l}}{g}} \)
+ Vận dụng tỉ số thời gian nén trên chu kì => tỉ lệ => Biên độ
+ Sử dụng vòng tròn lượng giác và biểu thức: \(\Delta \varphi = \omega \Delta t\)

