Một con lắc lò xo gồm vật nhỏ có khối lượng \(m = 300g\) treo vào một lò xo nhẹ có độ cứng \(k = 120N/m\). Kéo vật theo phương thẳng đứng xuống dưới vị trí cân bằng một đoạn \(2,5\sqrt 2 cm\), rồi truyền cho nó vận tốc \(50\sqrt 2 cm/s\) theo phương thẳng đứng, chiều dương hướng lên. Biết vận dao động điều hòa theo phương thẳng đứng trùng với trục của lò xo. Cho \(g = {\pi ^2} = 10m/{s^2}\). Xác định khoảng thời gian từ lúc bắt đầu dao động đến lúc vật qua vị trí mà lò xo dãn \(2,5cm\) đầu tiên đầu tiên.
Trả lời bởi giáo viên
Chu kì dao động của vật: \(T = 2\pi \sqrt {\dfrac{m}{k}} = 2\pi \sqrt {\dfrac{{0,3}}{{120}}} = 0,1\pi {\rm{s}}\)
Tần số góc: \(\omega = \dfrac{{2\pi }}{T} = 20({\rm{r}}a{\rm{d}}/s)\)
Biên độ dao động: \(A = \sqrt {{x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}} = \sqrt {{{\left( {2,5\sqrt 2 } \right)}^2} + \dfrac{{{{(50\sqrt 2 )}^2}}}{{{{(20)}^2}}}} = 5cm\)
Độ dãn của lò xo tại VTCB: \(\Delta l = \dfrac{{mg}}{k} = \dfrac{{0,3.10}}{{120}} = 0,025m = 2,5cm\)
=> Vị trí lò xo dãn \(2,5cm\) là \(x = + \dfrac{A}{2}\)
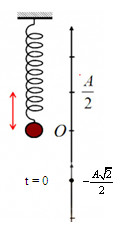
Thời gian từ lúc bắt đầu dao động đến lúc vật qua vị trí mà lò xo dãn \(2,5cm\) lần đầu tiên (khoảng thời gian vật đi từ \( - \dfrac{{A\sqrt 2 }}{2} \to \dfrac{A}{2}\)) là:
\(t = \dfrac{T}{8} + \dfrac{T}{{12}} = \dfrac{{5T}}{{24}} = \dfrac{5}{{24}}.0,1\pi = \dfrac{\pi }{{48}}s\)
Hướng dẫn giải:
+ Áp dụng biểu thức tính chu kì dao động của con lắc lò xo: \(T = 2\pi \sqrt {\dfrac{m}{k}} \)
+ Áp dụng biểu thức tính tần số góc: \(\omega = \dfrac{{2\pi }}{T}\)
+ Áp dụng hệ thức độc lập A-x-v: \({A^2} = {x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}}\)
+ Áp dụng biểu thức tính độ dãn tại VTCB của lò xo treo thẳng đứng: \(\Delta l = \dfrac{{mg}}{k}\)
+ Sử dụng trục thời gian suy ra từ vòng tròn

