Một con lắc lò xo treo thẳng đứng. Kích thích cho con lắc dao động điều hòa theo phương thẳng đứng. Chu kì và biên độ dao động của con lắc lần lượt là \(0,6s\) và \(6\sqrt 3 cm\). Chọn trục x’x thẳng đứng chiều dương hướng xuống, gốc tọa độ tại vị trí cân bằng, gốc thời gian \(t = 0\) khi vật qua vị trí cân bằng theo chiều dương. Lấy gia tốc rơi tự do \(g = 10m/{s^2}\) và \({\pi ^2} = 10\). Thời gian ngắn nhất kể từ khi \(t{\rm{ }} = {\rm{ }}0\) đến khi lực đàn hồi của lò xo có độ lớn cực tiểu là:
Trả lời bởi giáo viên
Ta có:
+ Độ dãn của lò xo tại VTCB: \(\Delta l = \dfrac{{mg}}{k} = \dfrac{g}{{{\omega ^2}}} = \dfrac{g}{{4{\pi ^2}}}{T^2} = \dfrac{{10}}{{4{\pi ^2}}}.{(0,6)^2} = 0,09m = 9cm\)
+ Biên độ \(A = 6\sqrt 3 cm\)
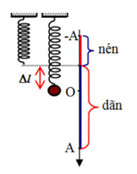
+ Vị trí lực đàn hồi của lò xo có độ lớn cực tiểu là: \(x = - \Delta l = - 9cm = - \dfrac{{A\sqrt 3 }}{2}\)
Tại t = 0: \(\left\{ \begin{array}{l}x = 0\\v > 0\end{array} \right.\)
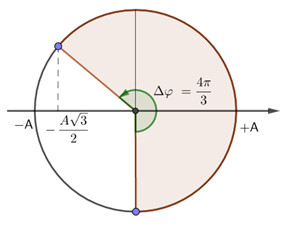
=> Thời gian ngắn nhất kể từ t = 0 đến khi lực đàn hồi của lò xo có độ lớn cực tiểu là thời gian vật đi từ \(0 \to A \to 0 \to - \dfrac{A}{2}\)
Ta có: \(\Delta \varphi = \dfrac{{4\pi }}{3} = \omega \Delta t\)
: \( \to \Delta t = \dfrac{{\Delta \varphi }}{\omega } = \dfrac{{\dfrac{{4\pi }}{3}}}{{\dfrac{{2\pi }}{T}}} = \dfrac{{2T}}{3} = \dfrac{{2.0,6}}{3} = 0,4s\)
Hướng dẫn giải:
+ Áp dụng biểu thức tính độ dãn tại VTCB của lò xo treo thẳng đứng: \(\Delta l = \dfrac{{mg}}{k}\)
+ Sử dụng trục thời gian suy ra từ vòng tròn

