Một con lắc lò xo treo thẳng đứng đao động điều hòa trên quỹ đạo dài \(30cm\). Biết rằng trong một chu kì tỉ số giữa thời gian lò xo giãn và thời gian lò xo nén bằng \({2}\). Lấy \(g{\rm{ }} = {\rm{ }}10m/{s^2}\) và \(\pi = 3,14\). Thế năng của con lắc biến thiên tuần hoàn với chu kì bằng:
Trả lời bởi giáo viên
Ta có:
- Chiều dài quỹ đạo \(L = 2A = 30cm \to A = 15cm\)
- Trong 1 nửa chu kì, tỉ số giữa thời gian lò xo giãn và thời gian lò xo nén là: \(\dfrac{{{t_{gian}}}}{{{t_{nen}}}} = \dfrac{{\dfrac{T}{2} - {t_{nen}}}}{{{t_{nen}}}} = 2 \to {t_{nen}} = \dfrac{T}{6}\)
Chọn chiều dương hướng xuống, ta có:
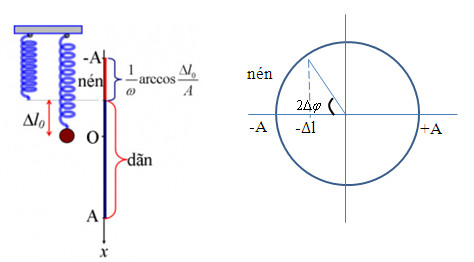
\(\begin{array}{l}\Delta \varphi = \omega .\Delta t = \dfrac{{2\pi }}{T}.\dfrac{T}{6} = \dfrac{\pi }{3}\\ \to \Delta l = Ac{\rm{os}}\dfrac{\pi }{3} = \dfrac{A}{2} = 7,5cm\end{array}\)
Mặt khác, ta có: \(\Delta l = \dfrac{{mg}}{k} = \dfrac{g}{{{\omega ^2}}} = \dfrac{g}{{4{\pi ^2}}}{T^2} = 0,075 \to T = \sqrt {\dfrac{{0,075.4{\pi ^2}}}{{10}}} = 0,544{\rm{s}}\)
Thế năng của con lắc biến thiên với chu kì: \(T' = \dfrac{T}{2} = \dfrac{{0,544}}{2} = 0,272s\)
Hướng dẫn giải:
+ Áp dụng công thức chiều dài quỹ đạo: L = 2A
+ Trong 1 nửa chu kì thì thời gian lò xo giãn: \({t_{gian}} = \dfrac{T}{2} - {t_{nen}}\)
+ Sử dụng vòng tròn lượng giác và công thức: \(\Delta \varphi = \omega .\Delta t\)
+ Vận dụng công thức tính độ dãn tại VTCB của lò xo treo thẳng đứng: \(\Delta l = \dfrac{{mg}}{k}\)

