Một lò xo có độ cứng k = 10N/m treo thẳng đứng. Treo lò xo vào một vật có khối lượng m = 250g. Từ vị trí cân bằng nâng vật lên một đoạn 50cm rồi buông nhẹ. Lấy g = π2 = 10m/s2. Tìm thời gian nén của con lắc lò xo trong một chu kì.
Trả lời bởi giáo viên
Biên độ dao động: A = 50cm
Độ dãn của lò xo tại VTCB: \(\Delta l = \frac{{mg}}{k} = \frac{{0,25.10}}{{10}} = 0,25m = 25cm\)
Chu kì dao động: \(T = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{0,25}}{{10}}} = 1{\rm{s}}\)
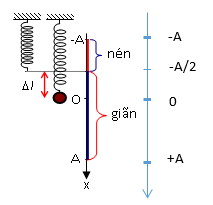
Chọn chiều dương hướng xuống:
=> Thời gian nén của lò xo trong một chu kì là: \({t_{nen}} = 2\frac{T}{6} = \frac{T}{3} = \frac{1}{3}s\)
Hướng dẫn giải:
+ Áp dụng biểu thức xác định độ dãn tại VTCB của con lắc lò xo treo thẳng đứng: \(\Delta l = \frac{{mg}}{k}\)
+ Áp dụng biểu thức tính chu kì dao động của con lắc lò xo: \(T = 2\pi \sqrt {\frac{m}{k}} \)
+ Sử dụng trục thời gian suy ra từ vòng tròn

