Ôn tập chương 3 - Dòng điện xoay chiều

Ta có

$\left\{ \begin{array}{l}\omega  = \dfrac{1}{{\sqrt {LC} }}\\{U_{RL}} = I.{Z_{RL}} = \dfrac{{U.{Z_{RL}}}}{Z} = \dfrac{{U.\sqrt {\left( {{R^2} + Z_L^2} \right)} }}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{U}{{\sqrt {1 + \dfrac{{Z_C^2 - 2{Z_L}{Z_C}}}{{{R^2} + Z_L^2}}} }}\end{array} \right.$

Từ biểu thức trên ta có để ${U_{RL}}$ không phụ thuộc vào $R$ ta suy ra:

${Z_C} = 2{Z_L} =  > \dfrac{1}{{\omega C}} = 2\omega L =  > \omega  = \dfrac{1}{{\sqrt 2 .\sqrt {LC} }} = \dfrac{{{\omega _0}}}{{\sqrt 2 }}$

+ Lúc đầu ta có ${U_L} = {\rm{ }}2{U_R}$ và điện áp toàn mạch $U = \sqrt {U_R^2 + {{\left( {{U_L} - {U_C}} \right)}^2}}  = 60\sqrt 2 V$

+ Lúc sau khi thay đổi tụ $C$ ta vẫn có $U{'_L} = 2U{'_R}$ ( do ${Z_L}$ và $R$ không đổi ).

Ngoài ra $U' = U$ nên:

$\begin{array}{l}U' = \sqrt {{U'_R}^2 + \left( {U{'_L} - U{'_C}}\right) ^2} = \sqrt {{U'_R}^2 + \left( {2U{'_R} - U{'_C}} \right)^2} = 60\sqrt 2 V\\ \to 60\sqrt 2 = \sqrt {{U'_R}^2 + \left( {2U{'_R} - 40} \right)^2} \\ \to U{'_R} = 53,1V\end{array}$

Ta có: $\tan \varphi  = \frac{{{Z_L}}}{r} = 1 =  > {\varphi _d} = \frac{\pi }{4}$

Mặt khác ta lại có ${\varphi _C} =  - \frac{\pi }{2}$

=> Độ lệch pha của hiệu điện thế giữa hai đầu cuộn dây và hai đầu tụ điện là $\frac{\pi }{4} - \left( { - \frac{\pi }{2}} \right) = \frac{{3\pi }}{4}$

+ Ta có: ${I_1} = {I_2} = \dfrac{{{I_0}}}{{\sqrt 2 }} \to {Z_1} = {Z_2}$

+ Vì $R$ không đổi $\to \dfrac{R}{{{Z_1}}} = \dfrac{R}{{{Z_2}}} \leftrightarrow c{\rm{os}}{\varphi _1} = c{\rm{os}}{\varphi _2}$

$\to \left[ \begin{gathered} {\varphi _1} = {\varphi _2}(loai) \hfill \\ {\varphi _1} = - {\varphi _2} \hfill \\ \end{gathered} \right.$

Với $\varphi$ - độ lệch pha của $u$ và $i$

Ta suy ra: $\varphi  = {\varphi _u} - {\varphi _{{i_1}}} = {\varphi _{{i_2}}} - {\varphi _u}$ (do ${\varphi _1} =  - {\varphi _2}$ )

$\to {\varphi _u} = \dfrac{{{\varphi _{{i_1}}} + {\varphi _{{i_2}}}}}{2} = \dfrac{{\dfrac{\pi }{4} - \dfrac{\pi }{{12}}}}{2} = \dfrac{\pi }{{12}}rad$

+ Điện áp cực đại ${U_0} = U\sqrt 2  = 60\sqrt 2 V$

=> Biểu thức điện áp $u = 60\sqrt 2 {\rm{cos}}\left( {100\pi t + \dfrac{\pi }{{12}}} \right)V$

Ta có hiệu điện thế $2$  đầu tụ ${U_C} = I.{Z_C} = \frac{{U.{Z_C}}}{Z} = \frac{{U.{Z_C}}}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}$

Thay đổi $L$ để ${U_C}$ đạt cực đại thì ${Z_L} = {\rm{ }}{Z_C}$

Ta có: ${U_L} = I.{Z_L} = \frac{U}{Z}{Z_L} = \frac{U}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}{Z_L}$  

Vì $R$ thay đổi nên để hiệu điện thế hai đầu cuộn cảm đạt cực đại thì $R$  tiến về $0$

+ Ta có: $\left\{ \begin{array}{l}R = 20\Omega \\{Z_L} = \omega L = 2\pi f.L = 2\pi .50.\dfrac{{0,4}}{\pi } = 40\Omega \end{array} \right.$  

+ C biên thiên để ${U_{{R_{{\rm{max}}}}}}$ => mạch cộng hưởng ${Z_L} = {Z_C} = 40\Omega$

+ Lại có ${Z_C} = \dfrac{1}{{\omega C}} \to C = \dfrac{1}{{\omega {Z_C}}} = \dfrac{1}{{2\pi f.{Z_C}}} = \dfrac{1}{{2\pi .50.40}} = \dfrac{{{{2,5.10}^{ - 4}}}}{\pi }F$

+ Ta có: $\left\{ \begin{array}{l}R = 50\Omega \\{Z_C} = \frac{1}{{\omega C}} = \frac{1}{{2\pi f.C}} = \frac{1}{{2\pi .50.\frac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \end{array} \right.$

Ta có: ${U_{RL}} = I{Z_{RL}} = \frac{{U\sqrt {{R^2} + Z_L^2} }}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }} = \frac{{U\sqrt {{R^2} + Z_L^2} }}{{\sqrt {{R^2} + {Z_L}^2 - 2{Z_L}{Z_C} + {Z_C}^2} }} = \frac{U}{{\sqrt {1 + \frac{{ - 2{Z_L}{Z_C} + {Z_C}^2}}{{{R^2} + Z_L^2}}} }}$

U_RLmax $\leftrightarrow {\left( {1 + \frac{{ - 2{Z_L}{Z_C} + {Z_C}^2}}{{{R^2} + Z_L^2}}} \right)_{\min }}$

$y = 1 + \frac{{ - 2{Z_L}{Z_C} + {Z_C}^2}}{{{R^2} + Z_L^2}}\\y' = (1 + \frac{{ - 2{Z_L}{Z_C} + {Z_C}^2}}{{{R^2} + Z_L^2}})' = \frac{{2{Z_L}^2 - 2{R^2} - 2{Z_L}{Z_C}}}{{{{({R^2} + Z_L^2)}^2}}}\\y' = 0 \leftrightarrow 2{Z_L}^2 - 2{R^2} - 2{Z_L}{Z_C} = 0$

Khi đó:

Khảo sát sự biến thiên của y ta được:

${y_{\max }} = \frac{{2RU}}{{\sqrt {4{{\rm{R}}^2} + Z_C^2}  - {Z_C}}}$ khi ${Z_L} = \frac{{{Z_C} + \sqrt {4{{\rm{R}}^2} + Z_C^2} }}{2}$

$\Rightarrow {Z_L} = \frac{{100 + \sqrt {{{4.50}^2} + {{100}^2}} }}{2} = 50.\left( {1 + \sqrt 2 } \right)\Omega$

Mà ${Z_L} = \omega L = 2\pi fL$

Suy ra $L = \frac{{{Z_L}}}{{2\pi f}} = \frac{{50\left( {1 + \sqrt 2 } \right)}}{{2\pi .50}} = \frac{{1,2}}{\pi } \approx 0,38H$

Đặt điện áp xoay chiều tần số f ở hai đầu cuộn sơ cấp. Nó gây ra sự biến thiên từ thông trong hai cuộn.

Gọi từ thông này là:   $\varphi {\rm{ }} = {\rm{ }}{\varphi _0}cos\omega t$

- Từ thông qua cuộn sơ cấp và thứ cấp lần lượt là :  ${\varphi _1} = {N_1}{\varphi _0}cos\omega t$ và  ${\varphi _2} = {N_2}{\varphi _0}cos\omega t$

- Trong cuộn thứ cấp xuất hiện suất điện động cảm ứng e₂ có biểu thức  ${e_2} =  - \dfrac{{d\Phi }}{{dt}} = {N_2}\omega {\Phi _0}\sin \omega t$ 

Từ đó ta thấy nguyên tắc hoạt động của máy biến áp dựa vào hiện tượng cảm ứng điện từ.

Vì máy biến thế là những thiết bị có khả năng biến đổi điện áp (xoay chiều) và không làm thay đổi tần số của nó.

Ta có: $\frac{{{U_1}}}{{{U_2}}} = \frac{{{N_1}}}{{{N_2}}} \to {U_1} = \frac{{{N_1}}}{{{N_2}}}{U_2} = \frac{{200}}{{100}}.200 = 400V$

Ta có hiệu suất máy biến áp là tỉ số giữa công suất của cuộn thứ cấp và cuộn sơ cấp nên:

$H = \frac{{{P_2}}}{{{P_1}}} = \frac{{{U_2}{I_2}\cos {\varphi _2}}}{{{U_1}{I_1}\cos {\varphi _1}}} = \frac{{20.6,2.0,8}}{{220.0,5.1}} = 0,9018 = 90,18\%$

+ Ta có :  $l = 2d = 20000{\rm{ }}m{\rm{ }},{\rm{ }}\rho  = {2,5.10^{ - 8}}\Omega .m{\rm{ }},S = {4.10^{ - 5}}m$

+ $R = \rho \dfrac{l}{S} = {2,5.10^{ - 8}}\dfrac{{20000}}{{{{4.10}^{ - 5}}}} = 12,5\Omega$

+ Công suất hao phí là: $\Delta P = \dfrac{{{P^2}}}{{{U^2}{\rm{co}}{{\rm{s}}^2}\varphi }}R$

=> Hiệu suất truyền tải điện là:

$\begin{array}{l}H = \dfrac{{P - \Delta P}}{P} = 1 - \dfrac{{\Delta P}}{P}\\ = 1 - \dfrac{P}{{{U^2}{\rm{co}}{{\rm{s}}^2}\varphi }} = 1 - \dfrac{{{{500.10}^3}}}{{{{\left( {{{10.10}^3}.0,9} \right)}^2}}}\\ = 0,9228 = 92,28\% \end{array}$

+ Ta có: $\Delta P = \frac{{{P^2}}}{{{U^2}{\rm{co}}{{\rm{s}}^2}\varphi }}R$

Vì công suất truyền đi, hệ số công suất và công suất hao phí trên đường dây không đổi nên khi tăng điện áp nơi truyền lên $2,5$ lần thì $R' = 6,25{\rm{ }}R$

Mà $R = \rho \frac{l}{S}$

Ta suy ra: $S' = \frac{S}{{6,25}}$

=> tiết diện dây dẫn giảm $6,25$ lần

+ Khi $f = {f_1}$ thì  $P = \dfrac{{{U^2}.R}}{{\left( {{R^2}{\rm{ }} + {\rm{ }}{Z^2_C}} \right)}} = 10\left( 1 \right)$

+ Khi $f = {f_2} = 2{f_1}$ thì  $P{\rm{ }} = \frac{{{U^2}.R}}{{\left( {{R^2}{\rm{ }} + {\rm{ }}\dfrac{{{Z_C}^2}}{4}} \right)}} = 20\left( 2 \right)$

+ Khi $f = {f_3} = 3{f_1}$ thì  $P = \frac{{{U^2}.R}}{{\left( {{R^2}{\rm{ }} + {\rm{ }}\frac{{Z_C^2}}{9}} \right)}}\left( 3 \right)$

Lấy $\frac{{\left( 1 \right)}}{{(2)}}$ ta được :  ${Z_C}^2 = 2{R^2}\left( 4 \right)$

Từ (1)  $\to {U^2}.R = 10\left( {{R^2} + {Z_C}^2} \right)\left( 5 \right)$

Thế (4) và (5) vào (3) ta được: $P = 20,77W$

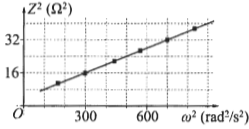
Từ đồ thị ta thấy với $\left\{ \begin{array}{l}{Z^2} = 32\left( {{\Omega ^2}} \right) \Rightarrow {\omega ^2} = 700\left( {ra{d^2}/{s^2}} \right)\\{Z^2} = 16\left( {{\Omega ^2}} \right) \Rightarrow {\omega ^2} = 300\,\,\left( {ra{d^2}/{s^2}} \right)\end{array} \right.$

Mà ${Z^2} = {R^2} + {\omega ^2}{L^2}$

Ta có hệ phương trình:

$\left\{ \begin{array}{l}16 = {R^2} + 300{L^2}\\32 = {R^2} + 700{L^2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}R = 2\left( \Omega  \right)\\L = 0,2\left( H \right)\end{array} \right.$

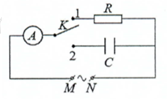
Cường độ dòng điện khi khóa K ở vị trí 1 và 2 là:

$\left\{ \begin{array}{l}{I_1} = I = \dfrac{U}{R}\\{I_2} = 2I = \dfrac{U}{{{Z_C}}}\end{array} \right. \Rightarrow \dfrac{1}{2} = \dfrac{{{Z_C}}}{R} \Rightarrow {Z_C} = \dfrac{R}{2} = \dfrac{{680}}{2} = 340\,\,\left( \Omega  \right)$

Dung kháng của tụ điện là:

${Z_C} = \dfrac{1}{{2\pi fC}} \Rightarrow 340 = \dfrac{1}{{2\pi .50.C}} \Rightarrow C = 9,{36.10^{ - 6}}\,\,\left( F \right)$

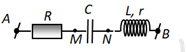
Ta có giản đồ vecto:

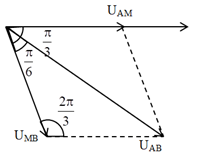
Từ giản đồ vecto, ta có định lí hàm sin:

$\dfrac{{{U_{AB}}}}{{\sin \dfrac{{2\pi }}{3}}} = \dfrac{{{U_{AM}}}}{{\sin \dfrac{\pi }{6}}} \Rightarrow {U_{AM}} = \dfrac{{{U_{AB}}\sin \dfrac{\pi }{6}}}{{\sin \dfrac{{2\pi }}{3}}} = \dfrac{{220\sin \dfrac{\pi }{6}}}{{\sin \dfrac{{2\pi }}{3}}} = 127\,\,\left( V \right)$

Dung kháng của tụ điện: ${Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{0,{{2.10}^{ - 3}}}}{\pi }}} = 50\,\,\left( \Omega  \right)$

Độ lệch pha giữa điện áp hai đầu đoạn mạch với cường độ dòng điện là:

$\begin{gathered} \tan \varphi = \frac{R}{{ - {Z_C}}} = \frac{{50}}{{ - 50}} \Rightarrow \varphi = - \frac{\pi }{4} = {\varphi _u} - {\varphi _i} \hfill \\ \Rightarrow {\varphi _i} = {\varphi _u} - \varphi = - \frac{\pi }{2} - \left( { - \frac{\pi }{4}} \right) = - \frac{\pi }{4}{\mkern 1mu} {\mkern 1mu} \left( {rad} \right) \hfill \\ \end{gathered}$

Nhận xét: Dòng điện sớm pha hơn điện áp giữa hai đầu tụ điện → pha ban đầu của điện áp giữa hai đầu tụ điện là: ${\varphi _{{u_C}}} = {\varphi _i} - \dfrac{\pi }{2} =  - \dfrac{\pi }{4} - \dfrac{\pi }{2} =  - \dfrac{{3\pi }}{4}$

Biểu thức điện áp giữa hai đầu tụ điện là:

${u_C} = {U_{0C}}\cos \left( {100\pi t - \dfrac{{3\pi }}{4}} \right)\,\,\left( V \right)$

Điện tích trên tụ điện bằng 0 khi điện áp giữa hai đầu tụ điện bằng 0:

$\begin{gathered} {u_C} = {U_{0C}}\cos \left( {100\pi t - \frac{{3\pi }}{4}} \right) = 0 \hfill \\ \Rightarrow 100\pi t - \frac{{3\pi }}{4} = - \frac{\pi }{2} \hfill \\ \Rightarrow t = {2,5.10^{ - 3}}{\mkern 1mu} {\mkern 1mu} \left( s \right) = 2,5{\mkern 1mu} {\mkern 1mu} \left( {ms} \right) \hfill \\ \end{gathered}$