Câu hỏi:
2 năm trước
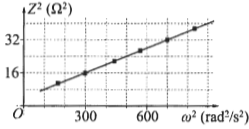
Trong giờ thực hành đo độ tự cảm của một cuộn dây, học sinh mắc nối tiếp cuộn dây đó với một điện trở thành một đoạn mạch. Đặt điện áp xoay chiều có tần số góc \(\omega \) thay đổi được vào hai đầu đoạn mạch rồi đo tổng trở Z của đoạn mạch. Hình bên là đồ thị biểu diễn sự phụ thuộc của \({Z^2}\) theo \({\omega ^2}.\) Độ tự cảm của cuộn dây bằng
Trả lời bởi giáo viên
Đáp án đúng: c
Từ đồ thị ta thấy với \(\left\{ \begin{array}{l}{Z^2} = 32\left( {{\Omega ^2}} \right) \Rightarrow {\omega ^2} = 700\left( {ra{d^2}/{s^2}} \right)\\{Z^2} = 16\left( {{\Omega ^2}} \right) \Rightarrow {\omega ^2} = 300\,\,\left( {ra{d^2}/{s^2}} \right)\end{array} \right.\)
Mà \({Z^2} = {R^2} + {\omega ^2}{L^2}\)
Ta có hệ phương trình:
\(\left\{ \begin{array}{l}16 = {R^2} + 300{L^2}\\32 = {R^2} + 700{L^2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}R = 2\left( \Omega \right)\\L = 0,2\left( H \right)\end{array} \right.\)
Hướng dẫn giải:
Cảm kháng của cuộn dây: \({Z_L} = \omega L\)
Tổng trở của mạch: \(Z = \sqrt {{R^2} + {Z_L}^2} = \sqrt {{R^2} + {\omega ^2}{L^2}} \)
Sử dụng kĩ năng đọc đồ thị
Câu hỏi khác
- Bài tập các mạch điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập mạch RLC mắc nối tiếp có lời giải MÔN LÝ lớp 12
- Bài tập pha u,i - viết phương trình u, i có lời giải MÔN LÝ lớp 12
- Bài tập lý thuyết đại cương về dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
- Bài tập đại cương dòng điện xoay chiều có lời giải MÔN LÝ lớp 12
