Cho ΔABC nội tiếp đường tròn (O;R)có độ dài các cạnh là AB=c,BC=a,CA=b kẻ AH⊥BC,AO cắt (O) tại D. Diện tích S của ΔABC là:
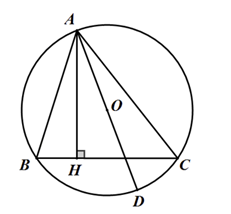
Xét ΔABH và ΔADCcó ^AHB=^ACD=900.
Các góc ^ABC,^ADC là các góc nội tiếp cùng chắn cung AC nên ^ABC=^ADC.
Do đó ΔABH∽ΔADC.
Vì vậy ABAD=AHAC⇒AH=AB.ACAD=bc2R.
Diện tích tam giác ABC là:
S=12AH.BC=12(bc2R).a=abc4R.
Cho nửa đường tròn (O) đường kính AB và C là điểm chính giữa của cung AB.
Lấy điểm M thuộc cung BC và điểm N thuộc tia AM sao cho AN=BM.
Kẻ dây CD song song với AM. Gọi S1 S2 lần lượt là diện tích của tam giác ACN và ΔBCM. (hình vẽ)
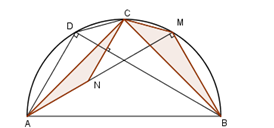
Chọn câu đúng.
Xét ΔACN và ΔBCM có:
+ AC=BC (vì C là điểm chính giữa của cung AB)
+ ^CAN=^CBN (hai góc nội tiếp cùng chắn cung CM)
+ Theo giả thiết ta có AN=BM.
Do đó ΔACN=ΔBCM(c.g.c). Hai tam giác bằng nhau nên diện tích bằng nhau. Do đó S1=S2.
Cho nửa đường tròn (O) đường kính AB và C là điểm chính giữa của cung AB.
Lấy điểm M thuộc cung BC và điểm N thuộc tia AM sao cho AN=BM.
Kẻ dây CD song song với AM. Gọi S1 S2 lần lượt là diện tích của tam giác ACN và ΔBCM. (hình vẽ)

Khi đó tam giác CMN là tam giác
Theo chứng minh ở câu 14 ta có ΔACN=ΔBCM.Do đóCN=CM.
Vì vậy ΔCMN là tam giác cân tại C(1).
Lại có ^CMA=12sdAC=12.900=450⇒^CMN=450.
ΔCMN là tam giác cân tại Cnên ^CNM=^CMN=450. Tổng ba góc trong một tam giác bằng 1800. Nên ^CMN+^CNM+^MCN=1800⇒450+450+^MCN=1800.
Do đó ^MCN=900(2).
Từ (1) và (2) suy ra ΔCMN vuông cân tại C .
Cho đường tròn (O;R)và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung AB và CD vuông góc với nhau (C thuộc cung nhỏ AB). Vẽ đường kính DE. Cho biết thêm rằng R=1. Giá trị lớn nhất của biểu thức Q=MA+MB+MC+MD là:
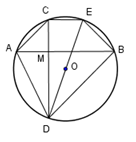
Do DE là đường kính của (O;R) nên ^DCE=900 (góc nội tiếp chắn nửa đường tròn).
Do đó CD⊥CE. Mặt khác theo giả thiết ta có CD⊥AB.
Do đó AB//CE.
Mặt khác các dây CE,AB là hai dây song song của (O) chắn hai cung AC và BE nên
cung AC bằng cung BE hay cùng AE bằng cung BC suy ra EA=BC.
Mặt khác ^DAE=900 (góc nội tiếp chắn nửa đường tròn).
Do đó MA2+MB2+MC2+MD2=(MA2+MD2)+(MB2+MC2)=AD2+BC2=DE2=4R2=4.
Áp dụng bất đẳng thức Cô-si cho MA2,MB2 ta có
MA2+MB2≥2MA.MB⇒2(MA2+MB2)≥2MA2+2MB2≥MA2+MB2+2MA.MB=(MA+MB)2.
Tương tự
2(MC2+MD2)≥(MC+MD)2.
Bằng cách tương tự trên ta chứng minh được
2[(MA+MB)2+(MC+MD)2]≥(MA+MB+MC+MD)2.
Từ đó ta suy ra 4(MA2+MB2+MC2+MD2)≥(MA+MB+MC+MD)2. Vì vậy
(MA+MB+MC+MD)2≤4.4=42⇒MA+MB+MC+MD≤4.
Dấu bằng xảy ra khi và chỉ khi MA=MB=MC=MD. Khi đó M≡O.
Cho hình vẽ ở bên. Giả sử rằng số đo các cung
AnC,CpD,DqB lần lượt có số đo là α,β,α(2α+β<3600).
Khi đó
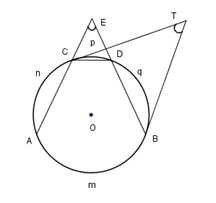
Theo giả thiết ta có sđAmB⏜
Theo tính chất góc có đỉnh nằm bên ngoài của đường tròn và áp dụng \left( 1 \right) ta có
\widehat {CED} = \dfrac{1}{2}\left( {sđ\,\overparen{AmB}\, - sđ\,\overparen{CpD}} \right) = \dfrac{1}{2}\left( {{{360}^0} - 2\alpha - \beta - \beta } \right) = {180^0} - \alpha - \beta \,\,\left( 2 \right).
Ta cũng có \widehat {BTC} là góc có đỉnh ở ngoài đường tròn ( có hai cạnh đều là tiếp tuyến của đường tròn) nên
\widehat {BTC} = \dfrac{1}{2}\left( {sđ\,\overparen{CAB} - sđ\,\overparen{CDB}} \right) = \dfrac{1}{2}\left[ {\left( {sđ\,\overparen{AmB} + sđ\,\overparen{AnC}} \right) - \left( {sđ\,\overparen{CpD} + sđ\,\overparen{DqB}} \right)} \right]
= \dfrac{1}{2}\left[ {\left\{ {\left( {{{360}^0} - 2\alpha - \beta } \right) + \alpha } \right\} - \left( {\beta + \alpha } \right)} \right]
{\kern 1pt} = \dfrac{1}{2}\left( {{{360}^0} - 2\alpha - 2\beta } \right) = {180^0} - \alpha - \beta \,\,\left( 3 \right).
Từ \left( 2 \right) và (3) ta suy ra \widehat {CED} = \widehat {BTC}.
Cho hình vẽ ở bên. Biết rằng sđBmC = {80^0}, M là điểm chính giữa N và B,sđAqN = \dfrac{1}{2} sđNrC
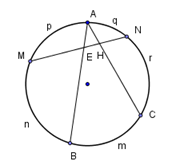
Khi đó ta có
Do tổng số đo tất cả các cung của đường tròn là {360^0}, hơn nữa ta có sd\,BmC = {80^0} nên ta có
sd\,BnM + sd\,MpA + sd\,AqN + sd\,NrC = {360^0} - {80^0} = {280^0}\,\,\left( 1 \right).
Mặt khác theo giả thiết ta cũng có
\left\{ \begin{array}{l}sd\,MpA + sd\,AqN = sd\,BnM\,\left( 2 \right)\\sd\,AqN = \dfrac{1}{2}sd\,NrC\,\left( 3 \right)\end{array} \right..
Thay \left( 3 \right) và \left( 2 \right) vào \left( 1 \right) ta nhận được
{280^0} = sd\,BnM + \left( {sd\,MpA + sd\,AqN} \right) + 2sd\,AqN = 2\left( {sd\,BnM + sd\,AqN} \right). Từ đây ta có
sd\,BnM + sd\,AqN = {140^0}. Suy ra \widehat {HEA} = \dfrac{1}{2}\left( {sd\,BnM + sd\,AqN} \right) = {70^0}\,\,\left( 4 \right).
Hơn nữa ta suy ra từ \left( 1 \right) rằng
\begin{array}{l}sd\,MpA + sd\,NrC = {280^0} - \left( {sd\,BnM + sd\,AqN} \right) = {280^0} - {140^0} = {140^0}\\ \Rightarrow \widehat {AHE} = \dfrac{1}{2}\left( {sd\,MpA + sd\,NrC} \right) = {70^0}\,\left( 5 \right).\end{array}
Từ \left( 4 \right) và \left( 5 \right) suy ra \Delta AEH cân tại A
Cho tứ giác ABCD nội tiếp đường tròn tâm O bán kính bằng a. Biết rằng AC \bot BD. Khi đó để AB + CD đạt giá trị lớn nhất thì
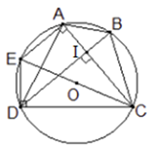
Vẽ đường kính CE của đường tròn \left( O \right).
Ta có \widehat {EAC} = {90^0},\,\widehat {EDC} = {90^0} (góc nội tiếp chắn đường kính EC ).
Từ đó ta có AE \bot AC. Mặt khác theo giả thiết AC \bot BD.
Kéo theo AE//BD. Vậy AEDB là hình thang.
Do hình thang AEDB nội tiếp \left( O \right) nên nói phải là hình thang cân.
Kéo theo AB = DE (các cạnh bên hình thang cân).
Từ đó ta có A{B^2} + C{D^2} = D{E^2} + D{C^2} = E{C^2} = {\left( {2a} \right)^2} = 4{a^2} (do \Delta EDC vuông tại D).
Áp dụng bất đẳng thức Cô-si cho cặp số \left( {A{B^2},B{D^2}} \right) ta có A{B^2} + B{D^2} \ge 2AB.CD \Rightarrow 2\left( {A{B^2} + B{D^2}} \right) \ge A{B^2} + B{D^2} + 2AB.CD = {\left( {AB + CD} \right)^2}.
Kéo theo {\left( {AB + CD} \right)^2} \le 2\left( {4{a^2}} \right) = 8{a^2} \Rightarrow AB + CD \le 2\sqrt 2 a.
Đẳng thức xảy ra khi và chỉ khi AB = CD.
Xét tam giác \Delta ABI,\,\,\Delta DCI có AB = CD, \widehat {ABD} = \widehat {ACD} (góc nội tiếp cùng chắn cung AD), \widehat {BAC} = \widehat {DCB} (góc nội tiếp cùng chắn cung BC).
Do đó\Delta ABI = \Delta DCI\left( {g.c.g} \right)
Kéo theo AI = ID,\,IB = IC. Suy ra AC = AI + IC = ID + IB = BD.
Cho tam giác ABC không cân, nội tiếp đường tròn \left( O \right),\,\,BD là đường phân giác của góc \widehat {ABC}.
Đường thẳng BD cắt đường tròn \left( O \right) tại điểm thứ hai là E. Đường tròn \left( {{O_1}} \right) đường kính DE cắt
đường tròn \left( O \right) tại điểm thứ hai là F. Khi đó đường thẳng đối xứng với đường thẳng BF qua đường thẳng BD cắt AC tại N thì:
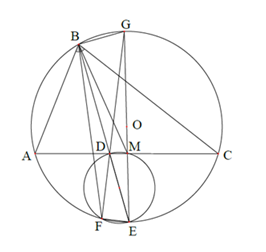
Gọi M là trung điểm của AC. Do E là điểm chính giữa cung AC nên EM \bot AC.
Do đó EM đi qua tâm của đường tròn \left( O \right). Giả sử rằng G = DF \cap \left( O \right). Do \widehat {DFE} = {90^0}, nên
\widehat {GFE} = {90^0}, hay GE là đường kính của \left( O \right). Suy ra G,M,E thẳng hàng.
Vì vậy \widehat {GBE} = {90^0}, mà \widehat {GMD} = {90^0}.
Kéo theo tứ giác BDMG là tứ giác nội tiếp đường tròn đường kính GD.
Vì vậy \widehat {MBD} = \widehat {DGM} = \widehat {FGE}\,\,\left( 1 \right)(cùng chắn cung DM)
Lại có tứ giác BFEG là tứ giác nội tiếp nên \widehat {FBE} = \widehat {FGE}\,\,\left( 2 \right)\, ( cùng chắn cung FE ).
Từ \left( 1 \right) và \left( 2 \right) ta suy ra \widehat {MBD} = \widehat {FBE}. Do đó BF và BM đối xứng nhau qua BD.
Vì vậy M \equiv N hay N là trung điểm của AC nên AN = NC.
Đầu xóm em có đào 1 cái giếng, miệng giếng hình tròn có đường kính 2m. Xung quanh miệng giếng người ta xây 1 cái thành rộng 0,4\left( m \right). Tính diện tích thành giếng là:
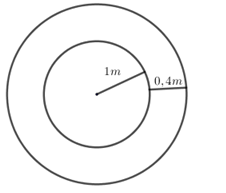
Quan sát hình vẽ, ta cần tính phần diện tích hình giới hạn bởi hai đường tròn.
Đường kính của giếng là 2\left( m \right) nên bán kính của giếng là 1\left( m \right).
Bán kính đường tròn ngoài là 1 + 0,4 = 1,4\left( m \right). Gọi {S_1},{S_2} lần lượt là diện tích của hình tròn nhỏ và lớn.
Khi đó ta có
{S_1} = \pi {.1^2} = \pi \,\left( {{m^2}} \right),{S_2} = \pi .{\left( {1,4} \right)^2} = 1,96\pi \,\left( {{m^2}} \right).
Diện tích của thành giếng là {S_2} - {S_1} = 1,96\pi - \pi = 0,96\pi \,\left( {{m^2}} \right).
Cho biết diện tích của hình quạt OAB bằng \dfrac{1}{4} diện tích của hình tròn. Khi đó \widehat {BOA} = ?
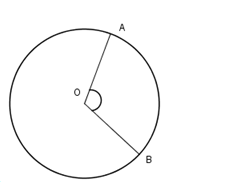
Đặt \alpha = \widehat {BOA}. Giả sử rằng R là bán kính của hình tròn. Khi đó ta có {S_{OAB}} = \dfrac{{\pi {R^2}}}{{360}}.\alpha .
Mặt khác diện tích của hình tròn là S = \pi {R^2}.
Theo giả thiết ta có {S_{OAB}} = \dfrac{1}{4}S \Rightarrow \dfrac{{\pi {R^2}}}{{360}}\alpha = \dfrac{1}{4}\left( {\pi {R^2}} \right) \Rightarrow \alpha = {90^0}.
Gọi M,\,N lần lượt là trung điểm của các cạnh AB,\,CD của hình chữ nhật ABCD. Biết rằng đường tròn ngoại tiếp hình chữ nhật ABCD có đường kính d = \sqrt {8 + 2\sqrt 3 } và tồn tại điểm I thuộc đoạn MN sao cho \widehat {DAI} = {45^0},\,\,\widehat {IDA} = {30^0}. Khi đó diện tích S của hình chữ nhật ABCD là:
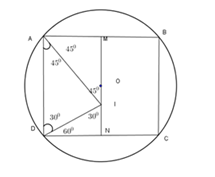
Theo giả thiết đường kính của đường tròn là \sqrt {8 + 2\sqrt 3 }
nên bán kính của đường tròn là R = \dfrac{{\sqrt {8 + 2\sqrt 3 } }}{2}.
Theo giả thiết \widehat A = {90^0},\widehat {DAI} = {45^0}, nên \widehat {IAM} = \widehat A - \widehat {DAI} = {90^0} - {45^0} = {45^0}. Do M,\,N là trung điểm
của các cạnh hình chữ nhật nên MN \bot AB. Do đó \widehat {AMI} = {90^0}.
Từ đó suy ra \widehat {AIM} = {45^0}. Vậy tam giác \Delta AMI vuông cân tại M.
Vì vậy AM = MI\,\,\left( 1 \right).
Do \widehat D = {90^0},\,\widehat {ADI} = {30^0} \Rightarrow \widehat {IDN} = {60^0}.
Từ đó \sin \,\widehat {IDN} = \dfrac{{IN}}{{DI}} \Rightarrow IN = \dfrac{{\sqrt 3 }}{2}DI. Tam giác DNI vuông tại N nên
D{I^2} = D{N^2} + I{N^2}. Do đó D{I^2} = D{N^2} + {\left( {\dfrac{{\sqrt 3 }}{2}DI} \right)^2} \Rightarrow DN = \dfrac{{DI}}{2}. Vì vậy IN = \sqrt 3 DN = \sqrt 3 AM\,\,\left( 2 \right).
Từ \left( 1 \right) và \left( 2 \right) ta có AD = MN = IM + IN = \left( {1 + \sqrt 3 } \right)AM = \dfrac{{1 + \sqrt 3 }}{2}AB.
Diện tích của hình chữ nhật là S = AB.AD = \dfrac{{1 + \sqrt 3 }}{2}A{B^2}\,\,\left( 3 \right).
Ta lại có
A{M^2} + O{M^2} = {R^2} \Leftrightarrow {\left( {\dfrac{{AB}}{2}} \right)^2} + {\left( {\dfrac{{AD}}{2}} \right)^2} = {R^2} \Leftrightarrow A{B^2} + A{D^2} = 4{R^2} \Leftrightarrow A{B^2} + {\left( {\dfrac{{1 + \sqrt 3 }}{2}AB} \right)^2} = 4{R^2}
\Leftrightarrow \dfrac{{8 + 2\sqrt 3 }}{4}A{B^2} = 4{R^2} = 4{\left( {\dfrac{{\sqrt {8 + 2\sqrt 3 } }}{2}} \right)^2} \Leftrightarrow AB = 2\,\,\left( 4 \right).
Từ \left( 3 \right) và \left( 4 \right) suy ra S = \dfrac{{1 + \sqrt 3 }}{2}.4 = 2\left( {1 + \sqrt 3 } \right).
Cho đường tròn \left( {O;R} \right) và một điểm M nằm ở ngoài đường tròn sao cho MO = 2R. Đường thẳng d đi qua M, tiếp xúc với đường tròn \left( {O;R} \right) tại A. Giả sử N = MO \cap \left( {O;R} \right). Kẻ hai đường kính AB,\,\,CD khác nhau của \left( {O;R.} \right) Các đường thẳng BC,\,BD cắt đường thẳng d lần lượt tại P,Q. Khi đó
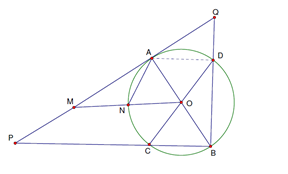
Xét \Delta QAB vuông ở A ta có AD \bot QB. Suy ra QB.DB = A{B^2} = 4{R^2} và QB.QD = A{Q^2}.
Ta có:
\begin{array}{l}QB > BD \Rightarrow {\left( {\sqrt {QB} - \sqrt {BD} } \right)^2} > 0\\ \Rightarrow BQ + BD > 2\sqrt {BQ.BD} = 4R\,\left( 3 \right).\end{array}
Tương tự ta có QB + QD > 2\sqrt {QB.QD} = 2AQ\,\,\left( 4 \right),
Cộng từng vế của \left( 3 \right) và \left( 4 \right) ta nhận được 2QB + DB + QD > 4R + 2AQ \Rightarrow 3QB - 2AQ > 4R.
Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax và By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax,\,By lần lượt tại C và D. Khi đó độ dài AC + BD nhỏ nhất khi:
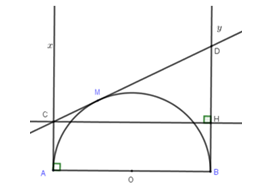
Do CM,\,DM là các tiếp tuyến nên ta có MD = BD,\,\,CM = CA.
Từ đó CA + BD = CM + MD = CD.
Từ C hạ đường cao CH xuống BD.
Khi đó \Delta HCD vuông tại H, có CD là cạnh huyền và CH là cạnh góc vuông nên CD \ge CH. Mặt khác CH//BA và CA \bot CH,\,\,BH \bot CH nên CHBA là hình chữ nhật.
Do đó CH = BA. Vì vậy CD \ge AB.
Do đó CA + BD nhỏ nhất khi và chỉ khi CA + BD = AB \Leftrightarrow CD = AB \Leftrightarrow CD = CH \Leftrightarrow CD//AB. Khi đó ta có ABDClà hình chữ nhật và do đó AC = BD. Mặt khác O là trung điểm AB nên M là trung điểm CD. Kéo theo CA = CM = MD = BD = R.
Cho hai đường tròn \left( {{O_1}} \right) và \left( {{O_2}} \right) có bán kính bằng R cắt nhau tại hai điểm A,\,B. Qua A vẽ cát tuyến cắt hai đường tròn \left( {{O_1}} \right) và \left( {{O_2}} \right) thứ tự tại E và F. \widehat {{O_2}A{O_1}} = {120^0}. Khi đó diện tích S phần giao của hai đường tròn \left( {{O_1}} \right) và \left( {{O_2}} \right) là:
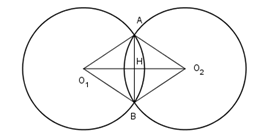
Gọi {S_1},\,{S_2},\,{S_3} lần lượt là diện tích của hình quạt A{O_2}B,\,A{O_1}B
và của tứ giác A{O_1}B{O_2}. Khi đó S ={S_1} + {S_2} - {S_3} và {S_1} = {S_2}.
Theo giải thiết ta có \widehat {{O_2}A{O_1}} = {120^0} nên \widehat {{O_2}AB} = \dfrac{1}{2}\widehat {{O_2}A{O_1}} = {60^0}.
Tam giác \Delta {O_2}AB cân tại {O_2} nên ta nhận được \Delta A{O_2}B là tam giác đều. Từ đó \widehat {A{O_2}B} = {60^0}.
Suy ra {S_1} = \dfrac{{\pi {R^2}}}{{360}}.60 = \dfrac{{\pi {R^2}}}{6}.
Gọi H = {O_1}{O_2} \cap AB.
Xét tam giác AHO{_2} vuông tại H. Ta có \widehat {HA{O_2}} = {60^0}, nên \sin \,{60^0} = \dfrac{{H{O_2}}}{{A{O_2}}} \Rightarrow H{O_2} = A{O_2}\sin \,{60^0} = \dfrac{{\sqrt 3 }}{2}R.
Áp dụng định lý Py-ta-go trong tam giác vuông AH{O_2} ta nhận được A{H^2} + {O_2}{H^2} = {O_2}{A^2} \Rightarrow A{H^2} = {O_2}{A^2} - {O_2}{H^2} = \dfrac{{{R^2}}}{4} \Rightarrow AH = \dfrac{R}{2}.
Diện tích tam giác AH{O_2} là \dfrac{1}{2}AH.H{O_2} = \dfrac{1}{2}.\left( {\dfrac{R}{2}} \right)\left( {\dfrac{{\sqrt 3 R}}{2}} \right) = \dfrac{{\sqrt 3 {R^2}}}{8}. Ta có thể kiểm tra được các tam giác \Delta AH{O_2},\,\Delta BH{O_2},\,\Delta AH{O_1},\,\Delta BH{O_1} là các tam giác bằng nhau. Do đó diện tích của tứ giác A{O_2}B{O_1} bằng 4 lần diện tích tam giác AH{O_2}. Do đó {S_3} = 4.\left( {\dfrac{{\sqrt 3 {R^2}}}{8}} \right) = \dfrac{{\sqrt 3 }}{2}{R^2}.
Từ đó ta có:
\begin{array}{l}S = {S_1} + {S_2} - {S_3}\\ = \dfrac{{\pi {R^2}}}{6} + \dfrac{{\pi {R^2}}}{6} - \dfrac{{\sqrt 3 {R^2}}}{2}\\ = \dfrac{{{R^2}\left( {2\pi - 3\sqrt 3 } \right)}}{6}\end{array}
Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax,\,By. Trên Ax lấy điểm M rồi kẻ tiếp tuyến MP cắt By tại N.Khi đó tỉ số \dfrac{{{S_{MON}}}}{{{S_{APB}}}} trong trường hợp AM = \dfrac{R}{2} là:
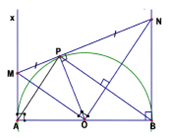
Theo tính chất hai tiếp tuyến cắt nhau ta có
OM là tia phân giác của góc \widehat {AOP} và ON là tia phân giác của góc \widehat {BOP}. Do đó \widehat {MOA} = \widehat {MOP},\,\,\widehat {PON} = \widehat {BON}\,\,\left( 1 \right).
Ta lại có \widehat {AOP},\,\widehat {BOP} là hai góc kề bù nên \widehat {AOP} + \,\widehat {BOP} = {180^0}\,\,\left( 2 \right).
Từ \left( 1 \right) và \left( 2 \right) ta suy ra
\widehat {MON} = \widehat {MOP} + \widetilde {PON} = \dfrac{1}{2}\left( {\widehat {AOM} + \widehat {MOP} + \widehat {PON} + \widehat {NOB}} \right)
= \dfrac{1}{2}\left( {\widehat {AOP} + \widehat {POB}} \right) = \dfrac{1}{2}{.180^0} = {90^0}\,\,.
Nên tam giác MON là tam giác vuông tại O có OP \bot MN (OP là tiếp tuyến).
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông MON ta có O{P^2} = PN.PM.
Ta lại có OP = R,\,AM = PM,\,BN = NP (tính chất hai tiếp tuyến cắt nhau).
Do đó AM.BN = {R^2}.
hay PN.PM = {R^2}
Mà PM = AM = \dfrac{R}{2} \Rightarrow PM = \dfrac{R}{2} \Rightarrow PN = 2R.
Do đó MN = PM + PN = \dfrac{R}{2} + 2R = \dfrac{{5R}}{2} \Rightarrow \dfrac{{MN}}{{AB}} = \dfrac{{\dfrac{{5R}}{2}}}{{2R}} = \dfrac{5}{4}
Ta có có \widehat {APB} là góc nội tiếp chắn nửa đường tròn nên \widehat {APB} = {90^0}\,\,\left( 4 \right).
Theo tính chất hai tiếp tuyến ta có
NB \bot ON \Rightarrow \widehat {OBN} = {90^0},\,\,NP \bot OP \Rightarrow \widehat {OPN} = {90^0} \Rightarrow \widehat {OBN} + \widehat {OPN} = {180^0}.
Do đó tứ giác OBNP là tứ giác nội tiếp. Từ đó \widehat {OBP} = \widehat {PNO}\,\,\left( 5 \right).
Từ \,\left( 4 \right); \left( 5 \right) và \widehat {MON} = 90^\circ suy ra hai tam giác vuông APB và MON đồng dạng với nhau.
Suy ra \dfrac{{{S_{MON}}}}{{{S_{APB}}}} = {\left( {\dfrac{{MN}}{{AB}}} \right)^2} = {\left( {\dfrac{5}{4}} \right)^2} = \dfrac{{25}}{{16}}.
Cho tam giác ABC cân tại A, nội tiếp đường tròn \left( {O;R} \right). Gọi D là trung điểm của AC; tia BD cắt tiếp tuyến tại A với đường tròn \left( O \right) tại điểm E;\,EC cắt \left( O \right) tại F. Giả sử rằng DF//BC. Khi đó cos\,\widehat {ABC} = ?
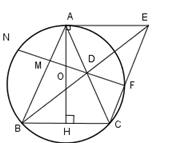
Giả sử rằng tia FD cắt AB tại M, cắt \left( O \right) tại N. Theo giả thiết DF//BC, và AH là trục đối xứng của BC và của đường tròn \left( O \right) nên F,\,D theo thứ tự là điểm đối xứng với N,\,M qua AH.
Do đó FD = MN = MD = \dfrac{1}{2}BC = \dfrac{1}{2}ND = BH\,\,\left( 1 \right).
Xét \Delta NDA,\,\Delta CDF có \widehat {ADN} = \widehat {CDF} (hai góc đối đỉnh).
\widehat {ACF},\,\widehat {FNA} là hai góc nội tiếp chắn cung AF nên \widehat {DCF} = \widehat {DNA}
Do đó \Delta NDA \backsim \Delta CDF \Rightarrow \dfrac{{DA}}{{DF}} = \dfrac{{ND}}{{CD}} \Rightarrow DF.DN = DA.DC\,\,\left( 4 \right).
Từ (1), (4) suy ra 2B{H^2} = \dfrac{1}{4}A{C^2} \Rightarrow BH = \dfrac{{\sqrt 2 }}{4}AC \Rightarrow \cos \,\widehat {ABC} = \dfrac{{BH}}{{AB}} = \dfrac{{BH}}{{AC}} = \dfrac{{\sqrt 2 }}{4}.
Cho A là điểm cố định trên đường tròn \left( {O;R} \right). Gọi AB và AC là hai dây cung thay đổi trên đường tròn \left( O \right) thỏa mãn \sqrt {AB.AC} = R\sqrt 3 . Khi đó vị trí của B,\,C trên \left( O \right) để diện tích \Delta ABC lớn nhất là:
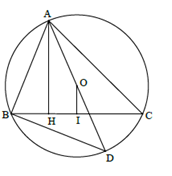
Kẻ AH \bot BC,\,OI \bot BC, đường kính AD.
Ta chứng minh được \Delta AHC \backsim \Delta ABD\,\left( {g - g} \right).
Do đó \dfrac{{AH}}{{AB}} = \dfrac{{AC}}{{AD}} \Rightarrow AH.AD = AB.AC \Rightarrow AB.AC = 2R.AH\,\,\left( 1 \right).
Theo giả thiết \sqrt {AB.AC} = R\sqrt 3 , nên AB.AC = 3{R^2}\,\,\left( 2 \right).
Thay \left( 2 \right) và \left( 1 \right) ta có AH = \dfrac{{3R}}{2}.
Lại có OI + OA \ge AI \ge AH nên OI \ge AH - OA = \dfrac{{3R}}{2} - R = \dfrac{R}{2}.
Do AH = \dfrac{{3R}}{2} là giá trị không đổi nên {S_{ABC}} lớn nhất khi BC lớn nhất \Leftrightarrow OI nhỏ nhất
\Leftrightarrow OI = \dfrac{R}{2} \Leftrightarrow BC \bot OA \Rightarrow \Delta ABC cân tại A.
Mà OI = \dfrac{R}{2} \Rightarrow \sin \widehat {OBI} = \dfrac{{OI}}{{OB}} = \dfrac{1}{2} \Rightarrow \widehat {OBI} = \widehat {OCI} = {30^0} \Rightarrow \widehat {BOC} = {120^0} \Rightarrow \widehat {BAC} = {60^0}
Vậy \Delta ABC đều.
Cho đường tròn \left( {O;R} \right), đường kính AB cố định, đường kính CD thay đổi\left( {CD \ne AB} \right). Các tia BC,\,BD cắt tiếp tuyến của đường tròn \left( O \right) tại A lần lượt tại E,\,F. Khi CD thay đổi. Giá trị nhỏ nhất của EF theo R là:
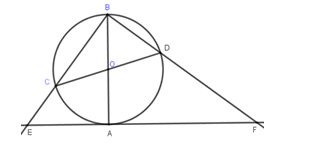
B\) thuộc đường tròn đường kính CD. Suy ra \widehat {DBC} = {90^0}.
Xét \Delta EBF có \widehat {EBF} = {90^0},\,BA \bot EF \Rightarrow AE.AF = A{B^2}.
Theo bất đẳng thức Cô-si cho \left( {AE,AF} \right) ta có
EF = AE + AF \ge 2\sqrt {AE.AF} = 2\sqrt {A{B^2}} = 2AB = 4R.
Vậy giá trị nhỏ nhất của EF là 4R. đạt được khi CD \bot AB.
Cho tam giác đều ABC có cạnh bằng 1, nội tiếp trong đường tròn tâm O. Đường cao AD của tam giác ABC cắt đường tròn tại điểm H. Diện tích phần giới hạn bởi cung nhỏ BC và hình BOCH là:
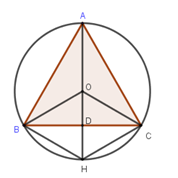
Ta có: AD là đường cao của \Delta ABC đều nên nó cũng là trung tuyến \Rightarrow BD = DC.
Xét \Delta DBH,\,\Delta DCH có
\begin{array}{l}BD = DC,\,\\\widehat {BDH} = \widehat {CDH} = {90^0}\\DH\,\,chung\end{array} \Rightarrow \Delta DBH = \,\Delta DCH\,\,\left( {c.g.c} \right) \Rightarrow BH = HC\,\,\left( 1 \right).
Do AH là đường kính nên \widehat {ACH} = {90^0}. Mà \widehat {ACD} = {60^0} \Rightarrow \widehat {DCH} = {30^0}
Do OA = OC = R nên \widehat {OAC} = \widehat {OCA} = {30^0} suy ra \widehat {OCD} = {30^0}
Xét hai tam giác vuông \Delta ODC,\Delta HDC có \widehat {ODC} = \widehat {HDC} = {90^0};\widehat {OCD} = \widehat {HCD} = {30^0};CD chung nên \Delta ODC = \Delta HDC\left( {g.c.g} \right) \Rightarrow OC = CH.
Tứ giác OBHC có 4 cạnh bằng nhau nên là hình thoi
Từ đó ta có OD = DH,\,BD = DC,\,\widehat {OCD} = {30^0},\,BC \bot OH nên:
\begin{array}{l}{S_1} = {S_{OBHC}} = \dfrac{1}{2}BC.OH = \dfrac{1}{2}\left( {2OD} \right)\left( {2DC} \right) = 2OD.DC\\ = 2\left( {OC.\sin \,\widehat {OCD}} \right)\left( {OC.\,\cos \,\widehat {OCD}} \right)\\ = 2O{C^2}\sin \,{30^0}\,.\cos \,{30^0} = {2.1^2}.\dfrac{1}{2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{\sqrt 3 }}{2}.\end{array}
Ta có diện tích hình quạt OBC là:
{S_2} = \dfrac{{\pi {R^2}}}{{360}}.120 = \dfrac{\pi }{3}.
Vậy diện tích cần tính là S = {S_1} - {S_2} = \dfrac{{\sqrt 3 }}{2} - \dfrac{\pi }{3}.
Cho tam giác ABC vuông tại A (AB < AC) nội tiếp trong đường tròn tâm O. Dựng đường thẳng d đi qua A song song với BC, đường thẳng d’ qua C song song BA, gọi D là giao điểm của d và d’. Dựng AE vuông góc với BD (E nằm trên BD), F là giao điểm của BD với đường tròn (O).
Tứ giác AECD nội tiếp đường tròn nào dưới đây:
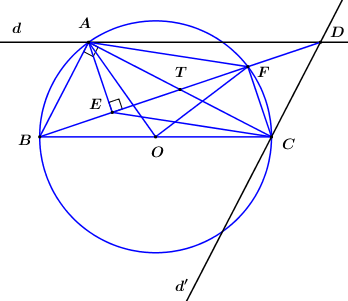
Vì \Delta ABC vuông tại A và nội tiếp \left( O \right) nên BC là đường kính của \left( O \right).
Ta có: \left\{ \begin{array}{l}AB \bot AC\\CD//AB\end{array} \right.\,\,\left( {gt} \right) \Rightarrow AC \bot CD (từ vuông góc đến song song) \Rightarrow \angle ACD = {90^0}.
Xét tứ giác AECD có: \angle AED = \angle ACD = {90^0} \Rightarrow AECD là tứ giác nội tiếp đường tròn đường kính AD. (Tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).

