Cho tam giác ABC vuông tại A (\(AB < AC\)) nội tiếp trong đường tròn tâm O. Dựng đường thẳng d đi qua A song song với BC, đường thẳng d’ qua C song song BA, gọi D là giao điểm của d và d’. Dựng AE vuông góc với BD (E nằm trên BD), F là giao điểm của BD với đường tròn (O).
Chọn khẳng định đúng:
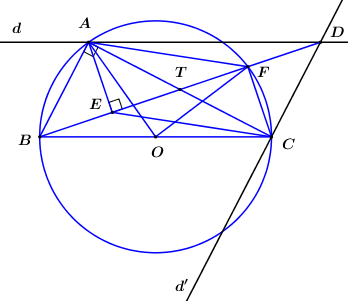
Do tứ giác \(AECD\) nội tiếp (cmt) nên: \(\angle CAE = \angle CDE\) (hai góc nội tiếp cùng chắn cung \(CE\))
Mà \(\angle CDE = \angle ABF\) (so le trong)
\( \Rightarrow \angle CAE = \angle ABF\).
Mặt khác: \(\angle AOF = 2\angle ABF\) (góc ở tâm và góc nội tiếp cùng chắn cung \(AF\))
\( \Rightarrow \angle AOF = 2\angle CAE\).
Cho tam giác ABC vuông tại A (\(AB < AC\)) nội tiếp trong đường tròn tâm O. Dựng đường thẳng d đi qua A song song với BC, đường thẳng d’ qua C song song BA, gọi D là giao điểm của d và d’. Dựng AE vuông góc với BD (E nằm trên BD), F là giao điểm của BD với đường tròn (O).
Tứ giác AECF là hình gì?
Do tứ giác \(AECD\) là tứ giác nội tiếp (cmt) nên: \(\angle ACE = \angle ADE\) (2 góc nội tiếp cùng chắn cung \(AE\)).
Ta có: \(\angle ADE = \angle DBC\) (so le trong do \(AD//BC\)) \( \Rightarrow \angle ACE = \angle DBC\).
Mà \(\angle DBC = \angle FBC = \angle FAC\) (hai góc nội tiếp cùng chắn cung \(FC\))
\( \Rightarrow \angle ACE = \angle FAC\). Mà hai góc này ở vị trí so le trong nên \(AF//EC\) (dhnb) (1)
Mặt khác: \(\angle CFE = {90^0}\) (góc nội tiếp chắn nửa đường tròn) nên \(CF \bot FE\) hay \(CF \bot BD\).
Mà \(AE \bot BD\,\,\left( {gt} \right)\) nên \(AE//CF\) (từ vuông góc đến song song) (2)
Từ (1) và (2) suy ra tứ giác \(AECF\) là hình bình hành (tứ giác có các cặp cạnh đối song song).
Cho tam giác ABC vuông tại A (\(AB < AC\)) nội tiếp trong đường tròn tâm O. Dựng đường thẳng d đi qua A song song với BC, đường thẳng d’ qua C song song BA, gọi D là giao điểm của d và d’. Dựng AE vuông góc với BD (E nằm trên BD), F là giao điểm của BD với đường tròn (O).
Chọn khẳng định đúng về tích DF.BD?
Gọi \(\left\{ T \right\} = AC \cap BD\).
Ta có: \(\left\{ \begin{array}{l}AB//CD\\AD//BC\end{array} \right.\,\,\left( {gt} \right) \Rightarrow ABCD\) là hình bình hành (dhnb) \( \Rightarrow TA = TC,\,\,TB = TD\) và \(AB = CD\) (tính chất).
Xét \(\Delta DCT\) vuông tại \(C\) có \(CF \bot BD\,\,\left( {cmt} \right) \Rightarrow CF \bot DT\) \( \Rightarrow CF\) là đường cao nên:
\(C{D^2} = DF.DT\) (hệ thức lượng trong tam giác vuông)
\( \Rightarrow 2.C{D^2} = 2.DF.DT = \left( {2.DT} \right).DF = DB.DF\).
Mà \(AB = CD\) (cmt).
Vậy \(DF.DB = 2A{B^2}\).
Cho tam giác nhọn \(ABC\) \(\left( {AB < AC} \right)\), các đường cao \(BD,\,\,CE\) \(\left( {D \in AC,\,\,E \in AB} \right)\) cắt nhau tại \(H\).
Tứ giác \(BEDC\) nội tiếp đường tròn nào dưới đây:
Ta có: \(BD,\,\,CE\) là các đường cao của \(\Delta ABC\) nên \(\left\{ \begin{array}{l}BD \bot AC\\CE \bot AB\end{array} \right. \Rightarrow \angle BDC = \angle BEC = {90^0}\)
\( \Rightarrow BEDC\) là tứ giác nội tiếp đường tròn đường kính BC (Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh đối diện các góc bằng nhau).
Cho tam giác nhọn \(ABC\) \(\left( {AB < AC} \right)\), các đường cao \(BD,\,\,CE\) \(\left( {D \in AC,\,\,E \in AB} \right)\) cắt nhau tại \(H\).
Gọi \(M\) là trung điểm của \(BC\). Đường tròn đường kính \(AH\) cắt \(AM\) tại điểm \(G\) (\(G\) khác \(A\)). Chứng Chọn khẳng định đúng?
Ta có: \(\angle AEH = \angle ADH = {90^0} \Rightarrow \angle AEH + \angle ADH = {180^0}\)
\( \Rightarrow AEHD\) nội tiếp đường tròn đường kính \(AH\) (định nghĩa)
Mà đường tròn đường kính \(AH\) cắt \(AM\) tại \(G\).
\( \Rightarrow \) Năm điểm \(A,E,H,G,D\) cùng thuộc một đường tròn.
\( \Rightarrow \angle AGE = \angle ADE\) (2 góc nội tiếp cùng chắn cung \(AE\))
Mà \(\angle ABC = \angle ADE\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp \(BEDC\))
\( \Rightarrow \angle ABC = \angle AGE\).
Xét \(\Delta ABM\) và \(\Delta AGE\) có: \(\angle ABC = \angle AGE\) (cmt); \(\angle BAM\) chung.
\( \Rightarrow \Delta ABM \sim \Delta AGE\,\,\,\left( {g.g} \right)\)\( \Rightarrow \frac{{AE}}{{AM}} = \frac{{AG}}{{AB}}\) (2 cặp cạnh tương ứng tỉ lệ)
\( \Rightarrow AE.AB = AG.AM\)
Cho tam giác nhọn \(ABC\) \(\left( {AB < AC} \right)\), các đường cao \(BD,\,\,CE\) \(\left( {D \in AC,\,\,E \in AB} \right)\) cắt nhau tại \(H\).
Hai đường thẳng \(DE\) và \(BC\) cắt nhau tại \(K\). Chọn khẳng định đúng?
Ta có \(\angle AGD = \angle AED\) (2 góc nội tiếp cùng chắn cung \(AD\))
Mà \(\angle AED = \angle ACB\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp \(BEDC\))
\( \Rightarrow \angle AGD = \angle ACB = \angle DCM\).
Lại có \(\angle AGD + \angle DGM = {180^0}\) (kề bù) \( \Rightarrow \angle DGM + \angle DCM = {180^0}\).
\( \Rightarrow GDCM\) là tứ giác nội tiếp (dhnb) \( \Rightarrow \angle MGC = \angle MDC\) (hai góc nội tiếp cùng chắn cung \(MC\)).
Lại có \(DM = \frac{1}{2}BC = MC\) (định lí đường trung tuyến trong tam giác vuông) \( \Rightarrow \Delta MCD\) cân tại \(M\).
\( \Rightarrow \angle MDC = \angle MCD\) (2 góc ở đáy của tam giác cân).
\( \Rightarrow \angle MGC = \angle MCD = \angle MCA\).
Xét \(\Delta GCM\) và \(\Delta CAM\) có: \(\angle AMC\) chung ; \(\angle MAC = \angle GCM\) (cmt)
\( \Rightarrow \Delta GCM \sim \Delta CAM\,\,\left( {g.g} \right)\) \( \Rightarrow \angle MAC = \angle GCM\) (2 góc tương ứng)
Cho tam giác nhọn \(ABC\) \(\left( {AB < AC} \right)\), các đường cao \(BD,\,\,CE\) \(\left( {D \in AC,\,\,E \in AB} \right)\) cắt nhau tại \(H\).
Chọn khẳng định đúng về hai đường thẳng nối tâm hai đường tròn ngoại tiếp hai tam giác \(MBE,MCD\)
Ta có \(\angle ABC = \angle AGE\,\,\left( {cmt} \right)\) nên \(EBMG\) là tứ giác nội tiếp (tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện).
\( \Rightarrow \) Đường nối tâm hai đường tròn ngoại tiếp hai tam giác \(MBE,MCD\) là đường nối tâm hai đường tròn ngoại tiếp hai tứ giác \(GDCM\) và \(EBMG\).
Giao của hai tứ giác \(GDCM\) và \(EBMG\) là \(GM\).
\( \Rightarrow \) Đường nối tâm vuông góc với \(GM\,\,\left( * \right)\)
Gọi \(\left\{ F \right\} = AH \cap BC\) \( \Rightarrow AF \bot BC \Rightarrow \angle AFB = {90^0}\).
Mà \(\angle BDA = {90^0}\) \( \Rightarrow ADFB\) nội tiếp (tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).
\( \Rightarrow \angle BAC = \angle DFM\) (1) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).
Mà \(\angle EDH = \angle EAH\)(2) (Hai góc nội tiếp cùng chắn cung \(EH\)).
\(\angle HDM = \angle HBM = \angle DBM\) (\(DM\) là trung tuyến của \(\Delta BDC\) vuông tại \(D\) nên \(DM = \frac{1}{2}BC = BM\)).
\(\angle DBM = \angle HAD\) (Cùng phụ \(\angle ACB\))
\( \Rightarrow \angle HDM = \angle HAD\,\,\,\left( 3 \right)\)
Từ (1), (2) và (3) suy ra
\(\angle EDM = \angle EDH + \angle HDM = \angle EAH + \angle HAD = \angle BAC = \angle DFM = \angle KDM\)
Xét \(\Delta FDM\) và \(\Delta DKM\) có: \(\angle KMD\) chung; \(\angle DFM = \angle KDM\) (cmt)
\( \Rightarrow \Delta FDM \sim \Delta DKM\,\,\,\left( {g.g} \right)\) \( \Rightarrow \frac{{MD}}{{KM}} = \frac{{FM}}{{MD}} \Rightarrow M{D^2} = FM.KM\)
Có: \(\Delta GCM \sim \Delta CAM\,\,\left( {cmt} \right)\)\( \Rightarrow \frac{{MC}}{{AM}} = \frac{{GM}}{{MC}} \Rightarrow M{C^2} = MG.MA\)
Mà \(MD = MC\)(cmt) \( \Rightarrow FM.KM = MG.MA \Rightarrow \frac{{FM}}{{GM}} = \frac{{MA}}{{MK}}\)
\( \Rightarrow \Delta FGM \sim \Delta AKM\,\,\,\left( {c.g.c} \right)\)\( \Rightarrow \angle FGM = \angle AKM\) (2 góc tương ứng)
\( \Rightarrow AGFK\) là tứ giác nội tiếp (tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện).
\( \Rightarrow \angle AFK = \angle AGK = {90^0}\) (2 góc nội tiếp cùng chắn cung \(AK\)) \( \Rightarrow KG \bot AG\) hay \(KG \bot GM\) (**)
Từ (*) và (**) suy ra đường nối tâm hai đường tròn ngoại tiếp hai tam giác \(MBE,MCD\) song song với \(KG\).
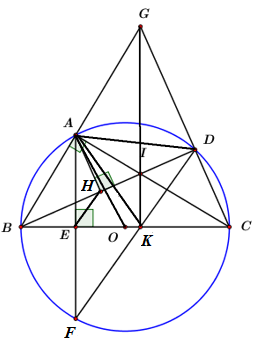
Cho \(\Delta ABC\,\,\,\left( {AB < AC} \right)\) nội tiếp đường tròn tâm \(O\) đường kính \(BC\) cố định, điểm \(D\) bất kì thuộc cung nhỏ \(AC\)\(\left( {D \ne A,\,\,D \ne C} \right).\) Tia \(BA\) cắt tia \(CD\) tại điểm \(G.\) Điểm \(I\) là giao điểm của \(BD\) và \(AC.\) Kẻ \(AE\) vuông góc với \(BC\) tại điểm \(E,\) đường thẳng \(AE\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(F.\) Gọi \(H\) là hình chiếu vuông góc của điểm \(A\) trên \(BD,\,\,K\) là giao điểm của \(BC\) và \(DF.\)
Tứ giác \(AIDG\) nội tiếp đường tròn nào sau đây?
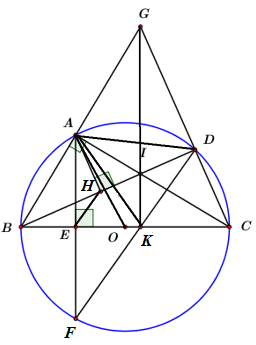
Ta có: \(\angle BAC,\)\(\angle BDC\) là góc nội tiếp chắn nửa đường tròn \(\left( O \right)\)\( \Rightarrow \angle BAC = \angle BDC = {90^0}.\)
\( \Rightarrow \angle GAI = \angle GDI = {90^0}\)
Xét tứ giác \(AIDG\) ta có: \(\angle GAI + \angle GDI = {90^0} + {90^0} = {180^0}\)
Suy ra \(AIDG\) là tứ giác nội tiếp đường tròn đường kính \(GI\).
Cho \(\Delta ABC\,\,\,\left( {AB < AC} \right)\) nội tiếp đường tròn tâm \(O\) đường kính \(BC\) cố định, điểm \(D\) bất kì thuộc cung nhỏ \(AC\)\(\left( {D \ne A,\,\,D \ne C} \right).\) Tia \(BA\) cắt tia \(CD\) tại điểm \(G.\) Điểm \(I\) là giao điểm của \(BD\) và \(AC.\) Kẻ \(AE\) vuông góc với \(BC\) tại điểm \(E,\) đường thẳng \(AE\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(F.\) Gọi \(H\) là hình chiếu vuông góc của điểm \(A\) trên \(BD,\,\,K\) là giao điểm của \(BC\) và \(DF.\)
Chọn khẳng định đúng:
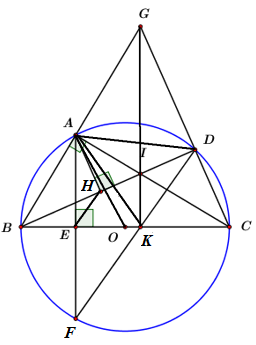
Xét tứ giác \(ABEH\) ta có: \(\angle AEB = \angle AHB = {90^0}\,\,\,\left( {gt} \right)\)
\( \Rightarrow ABEH\) là tứ giác nội tiếp. (tứ giác có hai đỉnh kề nhau cùng nhìn cạnh đối diện dưới các góc bằng nhau)
\( \Rightarrow \angle BHE = \angle BAE\) (hai góc nội tiếp cùng chắn cung \(BE\))
Mà \(\angle BAE = \angle BCA\) (hai góc cùng phụ \(\angle ABC\))
\( \Rightarrow \angle BHE = \angle BCA = \angle BCI\)
Xét \(\Delta BHE\) và \(\Delta BCI\) có:
\(\angle IBC\,\) chung
\(\angle BHE = \angle BCI\,\,\left( {cmt} \right)\)
\( \Rightarrow \dfrac{{BE}}{{BI}} = \dfrac{{BH}}{{BC}} \Rightarrow BE.BC = BH.BI\,\)
Cho \(\Delta ABC\,\,\,\left( {AB < AC} \right)\) nội tiếp đường tròn tâm \(O\) đường kính \(BC\) cố định, điểm \(D\) bất kì thuộc cung nhỏ \(AC\)\(\left( {D \ne A,\,\,D \ne C} \right).\) Tia \(BA\) cắt tia \(CD\) tại điểm \(G.\) Điểm \(I\) là giao điểm của \(BD\) và \(AC.\) Kẻ \(AE\) vuông góc với \(BC\) tại điểm \(E,\) đường thẳng \(AE\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(F.\) Gọi \(H\) là hình chiếu vuông góc của điểm \(A\) trên \(BD,\,\,K\) là giao điểm của \(BC\) và \(DF.\)
Chọn khẳng định đúng:
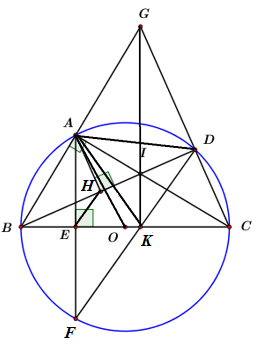
Xét \(\Delta BHE\) và \(\Delta BCI\) có:
Ta có: \(BC \bot AF \Rightarrow \,\,cung\,\,AB = cung\,\,FB\) (đường kính vuông góc với một dây thì đi qua điểm ở chính giữa của cung căng dây đó).
\( \Rightarrow \angle BDF = \angle BCA\) (hai góc nội tiếp chắn 2 cung bằng nhau).
Hay \(\angle IDK = \angle ICK\)
\( \Rightarrow CDJK\) là tức giác nội tiếp. (tứ giác có 2 đỉnh kề nhau cùng nhìn 1 cạnh dưới các góc bằng nhau)
\( \Rightarrow \angle IKC + \angle IDC = {180^0}\). Mà \(\angle IDC = \angle BDC = {90^0}\,\,\,\left( {cmt} \right)\)
\( \Rightarrow \angle IKC = {90^0} \Rightarrow IK \bot BC\,\,\,\left( 1 \right)\)
Xét \(\Delta GBC\) có \(\left\{ \begin{array}{l}AC \bot BG\\BD \bot CG\\AC \cap BD = \left\{ I \right\}\end{array} \right.\)
\( \Rightarrow I\) là trực tâm \(\Delta GBC\) \( \Rightarrow GI \bot BC\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) \( \Rightarrow G,\,\,I,\,\,K\) thằng hàng.
Cho \(\Delta ABC\,\,\,\left( {AB < AC} \right)\) nội tiếp đường tròn tâm \(O\) đường kính \(BC\) cố định, điểm \(D\) bất kì thuộc cung nhỏ \(AC\)\(\left( {D \ne A,\,\,D \ne C} \right).\) Tia \(BA\) cắt tia \(CD\) tại điểm \(G.\) Điểm \(I\) là giao điểm của \(BD\) và \(AC.\) Kẻ \(AE\) vuông góc với \(BC\) tại điểm \(E,\) đường thẳng \(AE\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(F.\) Gọi \(H\) là hình chiếu vuông góc của điểm \(A\) trên \(BD,\,\,K\) là giao điểm của \(BC\) và \(DF.\)
Đường tròn ngoại tiếp \(\Delta AKD\) luôn đi qua một điểm cố định khác \(A\) khi điểm \(D\) di động trên cung nhỏ \(AC\)?
Ta có: \(OA = \dfrac{1}{2}BC = OB\) (đường trung tuyến ứng với cạnh huyền trong tam giác vuông)
\( \Rightarrow \Delta OAB\) cân tại \(O\) \( \Rightarrow \angle OAB = \angle OBA = \angle ABC = \dfrac{1}{2}\,\,sd\,\,cung\,\,AC\) \(\left( 3 \right)\)
Lại có: \(\angle CKD = \dfrac{1}{2}\left( {sd\,\,cung\,\,CD + sd\,\,cng\,\,BF} \right)\)\( = \dfrac{1}{2}\left( {sd\,\,cung\,\,CD + sd\,\,cung\,\,AB} \right)\)
Vì \(OH \bot BD\,\,\left( {gt} \right)\)\( \Rightarrow cung\,\,AB = cung\,\,AD\)
\( \Rightarrow \angle CKD = \dfrac{1}{2}\left( {sd\,\,cung\,\,CD + \,sd\,\,cung\,\,AD} \right)\)\( = \dfrac{1}{2}sd\,\,cung\,\,AC\,\,\,\left( 4 \right)\)
Từ \(\left( 3 \right)\) và \(\left( 4 \right)\) \( \Rightarrow \angle OAB = \angle CKD\)
\( \Rightarrow OKDA\) là tứ giác nội tiếp. (tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện)
\( \Rightarrow \) Đường tròn ngoại tiếp \(\Delta AKD\) đi qua điểm \(O\) cố định.

