Tìm \(x\) sao cho \(\left| {\rm{Q}} \right| > {\rm{Q}}\).
Ta có \(\left| {\rm{Q}} \right|{\rm{ }} > {\rm{ Q }} \Leftrightarrow {\rm{ Q < 0}}\)
Khi đó ta được: \(\dfrac{x}{{2\left( {x - 1} \right)}}\) < 0 \(\forall x \ne \pm 1\)
TH1: \(\left\{ \begin{array}{l}x < 0\\x - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < 0\\x > 1\end{array} \right.\) không xảy ra.
TH2: \(\left\{ \begin{array}{l}x > 0\\x - 1 < 0\end{array} \right. \Leftrightarrow {\rm{ 0 < x < 1}}\).
Vậy với \({\rm{ 0 < x < 1}}\) thì \(\left| {\rm{Q}} \right|{\rm{ }} > {\rm{ Q}}\).
Tìm \(x\) biết \(Q = 3.\)
Theo kết quả câu trước \(Q = \dfrac{x}{{2\left( {x - 1} \right)}}\) với mọi \(x \ne \pm 1\).
Để \(Q = 3\) thì \(\dfrac{x}{{2\left( {x - 1} \right)}} = 3 \Rightarrow x = 3. 2\left( {x - 1} \right)\)
\( \Leftrightarrow x = 6x - 6 \Leftrightarrow 6x - x = 6 \Leftrightarrow 5x = 6\)\( \Leftrightarrow x = \dfrac{6}{5}\;\left( {tm} \right)\)
Vậy \(x = \dfrac{6}{5}\) thì \(Q = 3.\)
Rút gọn Q ta được:
\(Q = \left( {\dfrac{{{x^2} - 1}}{{x - 1}} + \dfrac{{{x^3} - 1}}{{1 - {x^2}}}} \right):\dfrac{{2{x^2} - 4x + 2}}{{{x^2} - 1}}\quad \left( {x \ne \pm 1} \right)\)
\(Q = \left( {\dfrac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{x - 1}} - \dfrac{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}} \right):\dfrac{{2{{\left( {x - 1} \right)}^2}}}{{{x^2} - 1}}\)
\(Q = \left( {\dfrac{{x + 1}}{1} - \dfrac{{{x^2} + x + 1}}{{x + 1}}} \right):\dfrac{{2\left( {x - 1} \right)}}{{x + 1}}\)
\(Q = \dfrac{{{{\left( {x + 1} \right)}^2} - {x^2} - x - 1}}{{x + 1}}.\dfrac{{x + 1}}{{2\left( {x - 1} \right)}}\)
\(\begin{array}{l}Q = \dfrac{{{x^2} + 2x + 1 - {x^2} - x - 1}}{{x + 1}}.\dfrac{{x + 1}}{{2\left( {x - 1} \right)}}\\Q = \dfrac{x}{{2\left( {x - 1} \right)}}\end{array}\)
Vậy \(Q = \dfrac{x}{{2\left( {x - 1} \right)}}\) với mọi \(x \ne \pm 1\).
Rút gọn Q ta được:
\(Q = \left( {\dfrac{{{x^2} - 1}}{{x - 1}} + \dfrac{{{x^3} - 1}}{{1 - {x^2}}}} \right):\dfrac{{2{x^2} - 4x + 2}}{{{x^2} - 1}}\quad \left( {x \ne \pm 1} \right)\)
\(Q = \left( {\dfrac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{x - 1}} - \dfrac{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}} \right):\dfrac{{2{{\left( {x - 1} \right)}^2}}}{{{x^2} - 1}}\)
\(Q = \left( {\dfrac{{x + 1}}{1} - \dfrac{{{x^2} + x + 1}}{{x + 1}}} \right):\dfrac{{2\left( {x - 1} \right)}}{{x + 1}}\)
\(Q = \dfrac{{{{\left( {x + 1} \right)}^2} - {x^2} - x - 1}}{{x + 1}}.\dfrac{{x + 1}}{{2\left( {x - 1} \right)}}\)
\(\begin{array}{l}Q = \dfrac{{{x^2} + 2x + 1 - {x^2} - x - 1}}{{x + 1}}.\dfrac{{x + 1}}{{2\left( {x - 1} \right)}}\\Q = \dfrac{x}{{2\left( {x - 1} \right)}}\end{array}\)
Vậy \(Q = \dfrac{x}{{2\left( {x - 1} \right)}}\) với mọi \(x \ne \pm 1\).
Trên các đoạn thẳng BD và CE lấy lần lượt hai điểm I và K sao cho \(\widehat {{\rm{AIC}}}{\rm{ = }}\widehat {{\rm{AKB }}}{\rm{ = 9}}{{\rm{0}}^{\rm{0}}}.\) Khi đó tam giác \(AIK\) là:
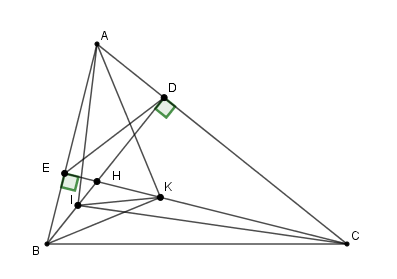
Xét \(\Delta AID\) và \(\Delta ACI\) có: \(\widehat {IAD}\) chung và \(\widehat {AIC} = \widehat {ADB} = {90^0}\) nên \(\Delta AID \backsim \Delta ACI\left( {g - g} \right)\)
Suy ra: \(\dfrac{{AI}}{{AC}} = \dfrac{{AD}}{{AI}} \Leftrightarrow A{I^2} = AC.AD\) (1)
Xét \(\Delta AEK\) và \(\Delta AKB\) có: \(\widehat {EAK}\) chung và \(\widehat {AIC} = \widehat {ADB} = {90^0}\) nên \(\Delta AEK \backsim \Delta AKB\left( {g - g} \right)\)
Suy ra: \(\dfrac{{AE}}{{AK}} = \dfrac{{AK}}{{AB}} \Leftrightarrow A{K^2} = AE.AB\) (2)
Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(\widehat {\rm{A}}\) là góc chung, \(\widehat {ADB} = \widehat {AEC} = {90^0}\)
\( \Rightarrow \) \(\Delta ABD \backsim \Delta ACE\left( {g - g} \right)\)
\( \Rightarrow \dfrac{{AD}}{{AE}} = \dfrac{{AB}}{{AC}}\) \( \Rightarrow AE.{\rm{ }}AB = AC.{\rm{ }}AD\) (3)
Từ (1), (2) và (3) suy ra: \(A{I^2} = A{K^2} \Rightarrow AI = AK\) nên tam giác \(AIK\) cân tại \(A.\)
Cho \(\widehat {{\rm{AED}}} = {40^0}\). Tính số đo \(\widehat {{\rm{HBC}}}\).
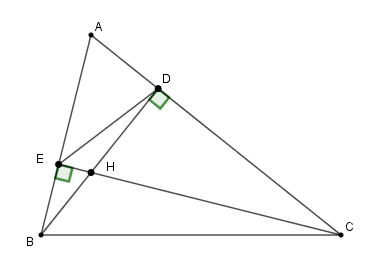
+) Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(\widehat {\rm{A}}\) là góc chung, \(\widehat {ADB} = \widehat {AEC} = {90^0}\)
\( \Rightarrow \) \(\Delta ABD \backsim \Delta ACE\) (g-g)
\( \Rightarrow \dfrac{{AD}}{{AE}} = \dfrac{{AB}}{{AC}}\)
Xét \(\Delta AED\) và \(\Delta ACB\) có: \(\widehat A\) chung và \(\dfrac{{AD}}{{AE}} = \dfrac{{AB}}{{AC}}\left( {cmt} \right)\) nên \(\Delta AED \backsim \Delta ACB\left( {c - g - c} \right)\)
Từ đó: \(\widehat {AED} = \widehat {ACB}\) (hai góc tương ứng)
Nên \(\widehat {ACB} = {40^0}\). Lại có: \(\Delta DBC\) vuông tại \(D\) nên \(\widehat {DCB} + \widehat {DBC} = {90^0}\)\( \Rightarrow \widehat {DBC} = {90^0} - {40^0} = {50^0}\)
Hay \(\widehat {HBC} = {50^0}\).
Hệ thức nào dưới đây đúng?
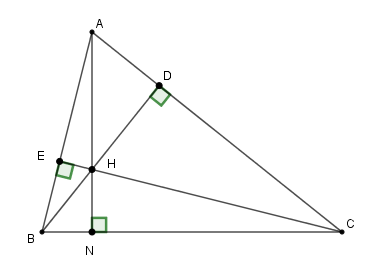
Kẻ \(AH\) cắt \(BC\) tại \(N.\) Vì \(H\) là giao điểm hai đường cao \(BD,CE\) nên \(H\) là trực tâm tam giác \(ABC.\)
Suy ra: \(AH \bot BC\) hay \(AN \bot BC.\)
Xét \(\Delta BHN\) và \(\Delta BCD\) có: \(\widehat B\) chung và \(\widehat {HNB} = \widehat {BDC} = {90^0}\) nên \(\Delta BHN \backsim \Delta BCD \left( {g - g} \right)\)
Suy ra: \(\dfrac{{BH}}{{BC}} = \dfrac{{BN}}{{BD}} \Rightarrow BH.BD = BN.BC\) (1)
Xét \(\Delta CHN\) và \(\Delta CBE\) có: \(\widehat C\) chung và \(\widehat {HNC} = \widehat {BEC} = {90^0}\) nên \(\Delta CHN \backsim \Delta CBE \left( {g - g} \right)\)
Suy ra: \(\dfrac{{CH}}{{CB}} = \dfrac{{CN}}{{CE}} \Rightarrow CH.CE = CN.BC\) (2)
Từ (1) và (2) suy ra \(BH.BD + CH.CE = BN.BC + CN.BC\)\( = BC\left( {CN + BN} \right) = BC.BC = B{C^2}\).
Vậy \(BH.BD + CH.CE = B{C^2}.\)
Tích \(AE{\rm{ }}.{\rm{ }}AB\;\) bằng:
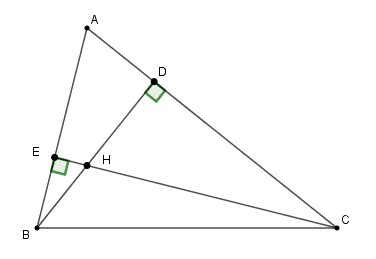
Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(\widehat {\rm{A}}\) là góc chung, \(\widehat {ADB} = \widehat {AEC} = {90^0}\)
\( \Rightarrow \) \(\Delta ABD \backsim \Delta ACE\) (g-g)
\( \Rightarrow \dfrac{{AD}}{{AE}} = \dfrac{{AB}}{{AC}}\)\( \Rightarrow AE.{\rm{ }}AB = AC. {\rm{ }}AD\).
Tích \(AE{\rm{ }}.{\rm{ }}AB\;\) bằng:

Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(\widehat {\rm{A}}\) là góc chung, \(\widehat {ADB} = \widehat {AEC} = {90^0}\)
\( \Rightarrow \) \(\Delta ABD \backsim \Delta ACE\) (g-g)
\( \Rightarrow \dfrac{{AD}}{{AE}} = \dfrac{{AB}}{{AC}}\)\( \Rightarrow AE.{\rm{ }}AB = AC. {\rm{ }}AD\).
Phân số nào có thể viết thành phân số thập phân?
Ta thấy: \(\dfrac{{12}}{{25}} = \dfrac{{12.4}}{{25.4}} = \dfrac{{48}}{{100}}\) nên nó là phân số thập phân.
Con hãy đọc đoạn văn và trả lời câu hỏi:
Nằm mơ
“Ôi lạ quá! Bỗng nhiên bé nhìn thấy mình biến thành cô bé tí hon. Những đóa hoa đang nở để đón mùa xuân. Còn bướm ong đang bay rập rờn. Nắng vàng làm những hạt sương lóng lánh. Thế mà bé cứ tưởng là bong bóng. Bé sờ vào, nó vỡ ra tạo thành một dòng nước cuốn bé trôi xuống đất. Bé sợ quá, thức dậy. Bé nói: “Thì ra mình nằm mơ.”

Bài văn tả mùa nào ?
c. Mùa xuân
c. Mùa xuân
c. Mùa xuân
Bài văn tả mùa xuân.
=> Đáp án: c
Phân số \(\dfrac{{35}}{{100}}\) viết dưới dạng số thập phân là:
Ta có: \(\dfrac{{35}}{{100}} = 0,35\).
Cho hình vẽ, biết \(DE// BC\). Khẳng định nào sau đây là đúng?
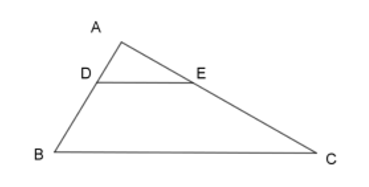
Áp dụng định lý Ta lét, ta có:
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} = \dfrac{{DE}}{{BC}}\)
\( \Rightarrow \) Đáp án A đúng.
Vì \(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\) nên \(AD.AC = AB.AE\)
\( \Rightarrow \) Đáp án B sai.
Ta có: \(\dfrac{{AD}}{{AB}} = \dfrac{{DE}}{{BC}}\)
\( \Rightarrow \)\(\dfrac{{AD}}{{AB - AD}} = \dfrac{{DE}}{{BC}} \Leftrightarrow \dfrac{{AD}}{{DB}} = \dfrac{{DE}}{{BC - DE}}\)
\( \Rightarrow \) Đáp án C sai.
Ta có: \(\dfrac{{AD}}{{AB}} = \dfrac{{DE}}{{BC}}\)
\( \Rightarrow AD.BC = AB.DE\)
\( \Rightarrow \) Đáp án D sai.
Con hãy đọc đoạn văn và trả lời câu hỏi:
Nằm mơ
“Ôi lạ quá! Bỗng nhiên bé nhìn thấy mình biến thành cô bé tí hon. Những đóa hoa đang nở để đón mùa xuân. Còn bướm ong đang bay rập rờn. Nắng vàng làm những hạt sương lóng lánh. Thế mà bé cứ tưởng là bong bóng. Bé sờ vào, nó vỡ ra tạo thành một dòng nước cuốn bé trôi xuống đất. Bé sợ quá, thức dậy. Bé nói: “Thì ra mình nằm mơ.”

Bướm ong đang bay như thế nào ?
b. Rập rờn
b. Rập rờn
b. Rập rờn
Bướm ong đang bay rập rờn.
=> Đáp án: b
Chữ số \(2\) trong số thập phân \(196,724\) có giá trị là:
Số thập phân \(196,724\) có chữ số \(2\) thuộc hàng phần trăm nên có giá trị là \(\dfrac{2}{{100}}\).
Khi \(x \ge 3\), kết quả rút gọn của biểu thức \(2{\rm{x}} + \left| {x - 3} \right| - 1\) là:
Khi \(x \ge 3\) thì \(\left| {x - 3} \right| = x - 3,\) ta có biểu thức:
\(2x + \left| {x - 3} \right| - 1 = 2x + x - 3 - 1 = 3x - 4.\)
Con hãy đọc đoạn văn và trả lời câu hỏi:
Nằm mơ
“Ôi lạ quá! Bỗng nhiên bé nhìn thấy mình biến thành cô bé tí hon. Những đóa hoa đang nở để đón mùa xuân. Còn bướm ong đang bay rập rờn. Nắng vàng làm những hạt sương lóng lánh. Thế mà bé cứ tưởng là bong bóng. Bé sờ vào, nó vỡ ra tạo thành một dòng nước cuốn bé trôi xuống đất. Bé sợ quá, thức dậy. Bé nói: “Thì ra mình nằm mơ.”

Bé tưởng cái gì là bong bóng ?
b. Những hạt sương lóng lánh
b. Những hạt sương lóng lánh
b. Những hạt sương lóng lánh
Bé tưởng những hạt sương lóng lánh là bong bóng.
=> Đáp án: b
Cho \(H = \left\{ {1;2;3;5;6} \right\}\).
Chọn cách viết đúng:
Nhận thấy \(3\) là phần tử thuộc tập hợp \(H\) nên ta có \(3 \in H.\)
Tìm hãy tìm tiếng có vần ay ?

Những
đóa
hoa
đang
nở
để
đón
mùa
xuân.
Còn
bướm
ong
đang
bay
rập
rờn.
Nắng
vàng
làm
những
hạt
sương
lóng
lánh.
Những
đóa
hoa
đang
nở
để
đón
mùa
xuân.
Còn
bướm
ong
đang
bay
rập
rờn.
Nắng
vàng
làm
những
hạt
sương
lóng
lánh.
Đáp án đúng là:
Những đóa hoa đang nở để đón mùa xuân. Còn bướm ong đang bay rập rờn. Nắng vàng làm những hạt sương lóng lánh.
\(\dfrac{3}{7}\) của \(21\) có giá trị là:
Ta có: \(\dfrac{3}{7}\) của \(21\) có giá trị là \(21\times \dfrac{3}{7} = 9\).

