Hệ thức nào dưới đây đúng?

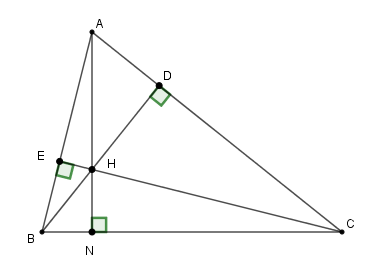
Kẻ $AH$ cắt $BC$ tại $N.$ Vì $H$ là giao điểm hai đường cao $BD,CE$ nên $H$ là trực tâm tam giác $ABC.$

Suy ra: $AH \bot BC$ hay $AN \bot BC.$

Xét $\Delta BHN$ và $\Delta BCD$ có: $\widehat B$ chung và $\widehat {HNB} = \widehat {BDC} = {90^0}$ nên $\Delta BHN \backsim \Delta BCD \left( {g - g} \right)$

Suy ra: $\dfrac{{BH}}{{BC}} = \dfrac{{BN}}{{BD}} \Rightarrow BH.BD = BN.BC$  (1)

Xét $\Delta CHN$ và $\Delta CBE$ có: $\widehat C$ chung và $\widehat {HNC} = \widehat {BEC} = {90^0}$ nên $\Delta CHN \backsim \Delta CBE \left( {g - g} \right)$

Suy ra: $\dfrac{{CH}}{{CB}} = \dfrac{{CN}}{{CE}} \Rightarrow CH.CE = CN.BC$ (2)

Từ (1) và (2) suy ra $BH.BD + CH.CE = BN.BC + CN.BC$$= BC\left( {CN + BN} \right) = BC.BC = B{C^2}$.

Vậy $BH.BD + CH.CE = B{C^2}.$