Trên các đoạn thẳng BD và CE lấy lần lượt hai điểm I và K sao cho $\widehat {{\rm{AIC}}}{\rm{  =  }}\widehat {{\rm{AKB }}}{\rm{ = 9}}{{\rm{0}}^{\rm{0}}}.$ Khi đó tam giác $AIK$ là:

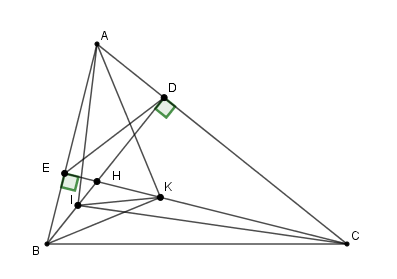
Xét $\Delta AID$ và $\Delta ACI$ có: $\widehat {IAD}$ chung và $\widehat {AIC} = \widehat {ADB} = {90^0}$ nên $\Delta AID \backsim \Delta ACI\left( {g - g} \right)$

Suy ra: $\dfrac{{AI}}{{AC}} = \dfrac{{AD}}{{AI}} \Leftrightarrow A{I^2} = AC.AD$  (1)

Xét $\Delta AEK$ và $\Delta AKB$ có: $\widehat {EAK}$ chung và $\widehat {AIC} = \widehat {ADB} = {90^0}$ nên $\Delta AEK \backsim \Delta AKB\left( {g - g} \right)$

Suy ra: $\dfrac{{AE}}{{AK}} = \dfrac{{AK}}{{AB}} \Leftrightarrow A{K^2} = AE.AB$ (2)

Xét $\Delta ABD$ và $\Delta ACE$ có:

$\widehat {\rm{A}}$ là góc chung, $\widehat {ADB} = \widehat {AEC} = {90^0}$

$\Rightarrow$ $\Delta ABD \backsim \Delta ACE\left( {g - g} \right)$

$\Rightarrow \dfrac{{AD}}{{AE}} = \dfrac{{AB}}{{AC}}$ $\Rightarrow AE.{\rm{ }}AB = AC.{\rm{ }}AD$ (3)

Từ (1), (2) và (3) suy ra: $A{I^2} = A{K^2} \Rightarrow AI = AK$ nên tam giác $AIK$ cân tại $A.$