Cho \(\widehat {{\rm{AED}}} = {40^0}\). Tính số đo \(\widehat {{\rm{HBC}}}\).

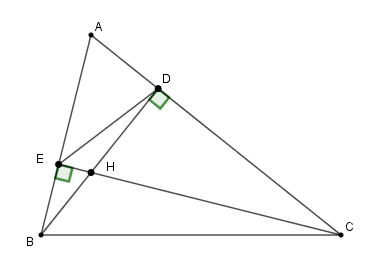
+) Xét \(\Delta ABD\) và \(\Delta ACE\) có:

\(\widehat {\rm{A}}\) là góc chung, \(\widehat {ADB} = \widehat {AEC} = {90^0}\)

\( \Rightarrow \) \(\Delta ABD \backsim \Delta ACE\) (g-g)

\( \Rightarrow \dfrac{{AD}}{{AE}} = \dfrac{{AB}}{{AC}}\)

Xét \(\Delta AED\) và \(\Delta ACB\) có: \(\widehat A\) chung và \(\dfrac{{AD}}{{AE}} = \dfrac{{AB}}{{AC}}\left( {cmt} \right)\) nên \(\Delta AED \backsim \Delta ACB\left( {c - g - c} \right)\)

Từ đó: \(\widehat {AED} = \widehat {ACB}\) (hai góc tương ứng)

Nên \(\widehat {ACB} = {40^0}\). Lại có: \(\Delta DBC\) vuông tại \(D\) nên \(\widehat {DCB} + \widehat {DBC} = {90^0}\)\( \Rightarrow \widehat {DBC} = {90^0} - {40^0} = {50^0}\)

Hay \(\widehat {HBC} = {50^0}\).