Phân tích đa thức \({x^3} + x{}^2 - 4x - 4\) thành nhân tử ta được:
\(\begin{array}{l}\,\,{x^3} + x{}^2 - 4x - 4\\ = {x^2}(x + 1) - 4(x + 1)\\ = ({x^2} - 4)(x + 1)\\ = (x - 2)(x + 2)(x + 1)\end{array}\)
Nhân dịp đầu năm học mới, nhà sách thực hiện chương trình giảm giá cho học sinh học sinh giỏi như sau: mỗi quyển loại 200 trang được giảm 5% còn mỗi quyển loại 120 trang được giảm 10%. Nếu năm học trước bạn Nam đạt danh hiệu học sinh giỏi thì bạn chỉ phải trả bao nhiêu tiền cho số vở trên.
Số tiền Nam được giảm khi mua 4 quyển vở loại 200 trang, 22 quyển vở loại 120 trang là:
\(13500. 4. 5\% {\rm{ }} + {\rm{ }}9500. 22. 10\% = 23600\) đồng.
Số tiền bạn phải trả nếu được giảm giá là:
\(263000--23600 = 239400\) (đồng).
Tính số vở loại \(120\) trang mà bạn Nam đã mua?
Gọi số quyển vở loại 200 trang bạn Nam mua là x (quyển, điều kiện \(x \in {\mathbb{N}^*},{\rm{ }}x < 26\) ) thì số quyển vở loại 120 trang là: \(26-x\) ( quyển)
Số tiền mua vở loại 200 trang là: \(13500x\) (đồng)
Số tiền mua vở loại 120 trang là: \(9500\left( {26 - x} \right)\) (đồng)
Vì bạn Nam đã trả tổng số tiền là \(263000\) đồng nên ta có phương trình \(13500x + 9500(26 - x) = 263000\)
\( \Leftrightarrow 13500x - 9500x = 263000 - 9500. 26\).
\( \Leftrightarrow 4000x = 16000\)\( \Leftrightarrow x = 4\) (thỏa mãn)
Vậy bạn Nam mua 4 quyển vở loại 200 trang, 22 quyển vở loại 120 trang.
Tính số vở loại \(120\) trang mà bạn Nam đã mua?
Gọi số quyển vở loại 200 trang bạn Nam mua là x (quyển, điều kiện \(x \in {\mathbb{N}^*},{\rm{ }}x < 26\) ) thì số quyển vở loại 120 trang là: \(26-x\) ( quyển)
Số tiền mua vở loại 200 trang là: \(13500x\) (đồng)
Số tiền mua vở loại 120 trang là: \(9500\left( {26 - x} \right)\) (đồng)
Vì bạn Nam đã trả tổng số tiền là \(263000\) đồng nên ta có phương trình \(13500x + 9500(26 - x) = 263000\)
\( \Leftrightarrow 13500x - 9500x = 263000 - 9500. 26\).
\( \Leftrightarrow 4000x = 16000\)\( \Leftrightarrow x = 4\) (thỏa mãn)
Vậy bạn Nam mua 4 quyển vở loại 200 trang, 22 quyển vở loại 120 trang.
Tính \(\widehat {BKE} + \widehat {BCE}\).
Tam giác \(EBA\) vuông cân tại \(A\) nên \(\widehat {BEA} = {45^0}.\)
Từ câu trước ta có: \(\Delta BEK \backsim \Delta CEB\)
Suy ra: \(\widehat {BKE} = \widehat {CBE}\)
Do đó: \(\widehat {BKE} + \widehat {BCE} = \widehat {CBE} + \widehat {BCE}\)
Ta lại có: \(\widehat {BEA}\)là góc ngoài của tam giác \(EBC\) nên \(\widehat {CBE} + \widehat {BCE} = \widehat {BEA} = {45^0}\)
Nên \(\widehat {BKE} + \widehat {BCE} = {45^0}.\)
Chọn câu đúng.
Từ câu trước ta có: \(\dfrac{{BE}}{{EK}} = \sqrt 2 ;\dfrac{{CE}}{{EB}} = \sqrt 2 \) suy ra: \(\dfrac{{BE}}{{EK}} = \dfrac{{CE}}{{EB}}\)
Xét tam giác \(\Delta BEK\)và \(\Delta CEB\) có:
+) \(\dfrac{{BE}}{{EK}} = \dfrac{{CE}}{{EB}}\)
+) \(\widehat {CEB}\) chung
Suy ra: \(\Delta BEK \backsim \Delta CEB\) (c – g - c)
Tính \(BE\) và các tỉ số \(\dfrac{{BE}}{{EK}};\) \(\dfrac{{CE}}{{EB}}\).
Vì \(AE = 2cm;AC = 6cm \Rightarrow EC = 4cm\)
Lại có \(K\) là trung điểm \(EC\) nên \(EK = KC = \dfrac{{EC}}{2} = 2cm\)
Ta có: \(AE = EK = KC = {\rm{ }}2cm\)
Xét tam giác \(ABE\) vuông tại \(A.\) Theo định lý Pytago ta có \(B{E^2} = A{B^2} + A{E^2}\)\( = {2^2} + {2^2} = 8\).
Suy ra: \(BE = 2\sqrt 2 \,cm\).
Từ đó suy ra: \(\dfrac{{BE}}{{EK}} = \dfrac{{2\sqrt 2 }}{2} = \sqrt 2 \) và \(\dfrac{{CE}}{{EB}} = \dfrac{4}{{2\sqrt 2 }} = \sqrt 2 \).
Tính \(BE\) và các tỉ số \(\dfrac{{BE}}{{EK}};\) \(\dfrac{{CE}}{{EB}}\).
Vì \(AE = 2cm;AC = 6cm \Rightarrow EC = 4cm\)
Lại có \(K\) là trung điểm \(EC\) nên \(EK = KC = \dfrac{{EC}}{2} = 2cm\)
Ta có: \(AE = EK = KC = {\rm{ }}2cm\)
Xét tam giác \(ABE\) vuông tại \(A.\) Theo định lý Pytago ta có \(B{E^2} = A{B^2} + A{E^2}\)\( = {2^2} + {2^2} = 8\).
Suy ra: \(BE = 2\sqrt 2 \,cm\).
Từ đó suy ra: \(\dfrac{{BE}}{{EK}} = \dfrac{{2\sqrt 2 }}{2} = \sqrt 2 \) và \(\dfrac{{CE}}{{EB}} = \dfrac{4}{{2\sqrt 2 }} = \sqrt 2 \).
Số \(5\dfrac{1}{4}\) gấp bao nhiêu lần số \(0,875\)
Đổi \(0,875 = \dfrac{{875}}{{1000}} = \dfrac{7}{8}\) và \(5\dfrac{1}{4} = \dfrac{{5 \times 4 + 1}}{4} = \dfrac{{21}}{4}\)
Ta có \(\dfrac{{21}}{4}:\dfrac{7}{8} = \dfrac{{21}}{4}.\dfrac{8}{7} = 6\)
Vậy số \(5\dfrac{1}{4}\) gấp \(6\) lần số \(0,875\)
Tính diện tích tam giác \(DMN,\) nếu biết diện tích tam giác \(ABC\) là: \(640\,c{m^2}.\)
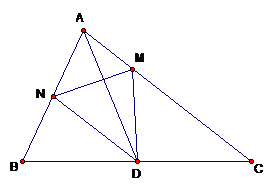
Nhận thấy hai tam giác \(ANC\) và \(ABC\) có chung chiều cao hạ từ đỉnh \(C\)
Mà \(AN = \dfrac{1}{2} \times AB\) nên \({S_{{\rm{ANC}}}} = \dfrac{1}{2}{S_{ABC}}{\rm{ }}\)
Nhận thấy hai tam giác \(ANM\) và \(ANC\) có chung chiều cao hạ từ đỉnh \(N\) mà \(AM = \dfrac{1}{3} \times AC\) nên \({{\rm{S}}_{{\rm{AMN}}}} = \dfrac{1}{3} \times {\rm{ }}{{\rm{S}}_{{\rm{ANC}}}}\).
Do đó: \({S_{AMN}} = \dfrac{1}{3} \times {S_{ANC}}\)\( = \dfrac{1}{3} \times \dfrac{1}{2} \times {S_{ABC}} = \dfrac{1}{6} \times {\rm{ }}{{\rm{S}}_{{\rm{ABC}}}}\)
Vậy \({S_{AMN}} = \dfrac{1}{6} \times {S_{ABC}}\)
Tương tự ta có: \({{\rm{S}}_{{\rm{DMC}}}} = \dfrac{1}{3} \times {{\rm{S}}_{{\rm{ABC}}}}{\rm{ ;\,}}{{\rm{S}}_{{\rm{DNB}}}} = \dfrac{1}{4} \times {{\rm{S}}_{{\rm{ABC}}}}\)
Mà \({S_{DMN}} + {S_{AMN}} + {S_{BDN}} + {S_{DCM}} = {S_{ABC}}\)
Nên \({S_{DMN}} = {S_{ABC}} - {S_{AMN}} - {S_{BDN}} - {S_{DCM}}\)\( = {S_{ABC}} - \dfrac{1}{6} \times {S_{ABC}} - \dfrac{1}{4} \times {S_{ABC}} - \dfrac{1}{3} \times {S_{ABC}} = \dfrac{1}{4} \times {S_{ABC}}\)
Do đó: \({S_{DMN}} = \dfrac{1}{4} \times {\rm{ }}{{\rm{S}}_{{\rm{ABC}}}} = \dfrac{1}{4} \times {\rm{ 640 = 160c}}{{\rm{m}}^{\rm{2}}}\)
Chọn câu đúng về diện tích hai tam giác \(ADM\) và \(ABC.\)
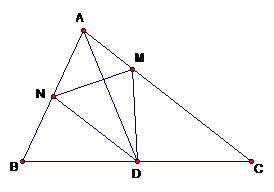
Nhận thấy hai tam giác \(ADC\) và \(ABC\) có chung chiều cao hạ từ đỉnh \(A\)
Mà \(BD = \dfrac{1}{2} \times BC\) nên \({S_{{\rm{ADC}}}} = \dfrac{1}{2}{S_{ABC}}{\rm{ }}\)
Nhận thấy hai tam giác \(ADM\) và \(ADC\) có chung chiều cao hạ từ đỉnh \(D\) mà \(AM = \dfrac{1}{3} \times AC\) nên \({{\rm{S}}_{{\rm{ADM}}}} = \dfrac{1}{3} \times {\rm{ }}{{\rm{S}}_{{\rm{ADC}}}}\).
Do đó: \({S_{ADM}} = \dfrac{1}{3} \times {S_{ADC}}\)\( = \dfrac{1}{3} \times \dfrac{1}{2} \times {S_{ABC}} = \dfrac{1}{6} \times {\rm{ }}{{\rm{S}}_{{\rm{ABC}}}}\)
Vậy \({S_{ADM}} = \dfrac{1}{6} \times {S_{ABC}}\)
Cho tập hợp \(A = \left\{ {x|12 \le x < 15} \right\}\). Viết tập hợp \(A\) dưới dạng liệt kê các phần tử.
Tập hợp \(A\) gồm các số tự nhiên lớn hơn hoặc bằng \(12\) và nhỏ hơn \(15\) tức là gồm các số \(12;13;14\)
Do đó \(A = \left\{ {12;13;14} \right\}\)
Tổng của 9 số tự nhiên liên tiếp từ 1 đến 9 có kết quả là:
Các số tự nhiên từ 1 đến 9 là: \(1,2,3,4,5,6,7,8,9\)
Tổng các số trên là: \(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9\)
\( = \left( {1 + 9} \right) + \left( {2 + 8} \right) + \left( {3 + 7} \right) + \left( {4 + 6} \right) + 5\)
\(\begin{array}{l} = 10 + 10 + 10 + 10 + 5\\ = 40 + 5 = 45\end{array}\)
Căn bậc hai số học của 4 là:
Vì \({2^2} = 4\) và \(2 > 0\) nên \(\sqrt 4 = 2.\)
So sánh 5 với \(2\sqrt 6 \) ta có kết luận sau:
Ta có: \({5^2} = 25;\,{\left( {2\sqrt 6 } \right)^2} = {2^2}.{\left( {\sqrt 6 } \right)^2} = 4.6 = 24\)
Vì \(25 > 24\) nên \(5 > 2\sqrt 6 .\)
Người ta cho một vòi nước chảy vào bể chưa có nước. Lần thứ nhất chảy vào \(\dfrac{3}{5}\) bể, lần thứ hai chảy vào thêm \(\dfrac{1}{3}\) bể. Hỏi còn mấy phần của bể chưa có nước?
Số phần bể chưa có nước là:
\(1 - \left( {\dfrac{3}{5} + \dfrac{1}{3}} \right) = \dfrac{1}{{15}}\) (bể)
\(\sqrt {{{\rm{x}}^2}} = 5\) thì \(x\) bằng:
Ta có: \(\sqrt {{{\rm{x}}^2}} = 5 \Leftrightarrow \left| x \right| = 5 \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = - 5\end{array} \right.\)
Chọn số thích hợp vào chỗ trống, biết: \(18,987 = 18 + 0,9 + \ldots + 0,007\)
Gọi số cần tìm là \(x\)
Ta có: \(18,987 = 18 + 0,9 + x + 0,007\)
\(\begin{array}{l}18,987 = 18,9 + x + 0,007\\18,987 = \left( {18,9 + 0,007} \right) + x\\18,987 = 18,907 + x\\x = 18,987 - 18,907\\x = 0,08\end{array}\)
Vậy số cần tìm là \(0,08.\)
Thực hiện phép tính sau \(\dfrac{{x - 3}}{{2x + 6}}:\left( {{x^2} - 6x + 9} \right)\), ta được kết quả là:
Ta có: \(\dfrac{{x - 3}}{{2x + 6}}:\left( {{x^2} - 6x + 9} \right) = \dfrac{{x - 3}}{{2(x + 3)}}.\dfrac{1}{{{{(x - 3)}^2}}} = \dfrac{1}{{2(x - 3)(x + 3)}} = \dfrac{1}{{2({x^2} - 9)}}\).
Nếu \(\Delta ABC\) vuông tại A có \(BH = 9,HC = 25\) thì đường cao \(AH\) có độ dài là:
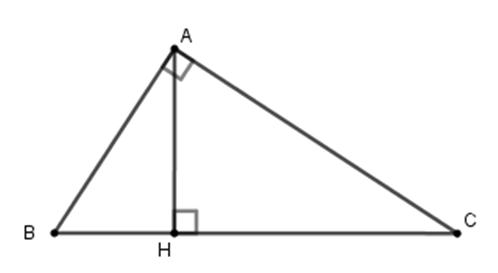
Xét tam giác \(ABC\) vuông tại \(A\) có chiều cao \(AH.\) Theo hệ thức lượng trong tam giác vuông ta có:
\(A{H^2} = HB.HC \Leftrightarrow A{H^2} = 9.25\) \( \Leftrightarrow A{H^2} = 225 \Rightarrow AH = 15\)
Vậy \(AH = 15\,cm.\)
