Cho tam giác $MNP$ vuông tại $M$. Khi đó $\cos \widehat {MNP}$ bằng

Ta có $\cos \widehat {MNP} = \dfrac{{MN}}{{NP}}$
Cho tam giác \(ABC\) vuông tại \(A,\,\,\angle ABC = {60^0},\) cạnh \(AB = 5cm.\) Độ dài cạnh \(AC\) là
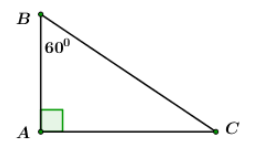
Xét tam giác \(ABC\) vuông tại \(A\) ta có:
\(\tan B = \dfrac{{AC}}{{AB}}\)
Suy ra \(AC = AB\tan B = 5.\tan {60^0} = 5\sqrt 3 \,\,cm.\)
\(B = \tan {10^0}.\tan {80^0} - \tan {20^0}.\tan {70^0}.\)
\(\,\,B = \tan {10^0}.\tan {80^0} - \tan {20^0}.\tan {70^0}.\)
Ta có:
\(\begin{array}{l}\,B = \tan {10^0}.\tan {80^0} - \tan {20^0}.\tan {70^0}\\\,\,\,\,\, = \tan {10^0}.\cot{10^0} - \tan {20^0}.\cot {20^0}\\\,\,\,\,\, = 1 - 1 = 0.\end{array}\)
\(A = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\sin ^2}{55^0} + {\sin ^2}{65^0} + {\sin ^2}{75^0}\)
\(\,\,A = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\sin ^2}55 + {\sin ^2}{65^0} + {\sin ^2}{75^0}\)
Ta có:
\(\begin{array}{l}A = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\sin ^2}55 + {\sin ^2}{65^0} + {\sin ^2}{75^0}\\\,\,\,\,\, = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\cos ^2}{35^0} + {\cos ^2}{25^0} + {\cos ^2}{15^0}\\\,\,\,\,\, = \left( {{{\sin }^2}{{15}^0} + {{\cos }^2}{{15}^0}} \right) + \left( {{{\sin }^2}{{25}^0} + {{\cos }^2}25} \right) + \left( {{{\sin }^2}{{35}^0} + {{\cos }^2}{{35}^0}} \right) + {\sin ^2}{45^0}\\\,\,\,\, = 1 + 1 + 1 + {\left( {\dfrac{{\sqrt 2 }}{2}} \right)^2} = 3 + \dfrac{1}{2} = \dfrac{7}{2}.\end{array}\)
\(A = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\sin ^2}{55^0} + {\sin ^2}{65^0} + {\sin ^2}{75^0}\)
\(\,\,A = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\sin ^2}55 + {\sin ^2}{65^0} + {\sin ^2}{75^0}\)
Ta có:
\(\begin{array}{l}A = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\sin ^2}55 + {\sin ^2}{65^0} + {\sin ^2}{75^0}\\\,\,\,\,\, = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\cos ^2}{35^0} + {\cos ^2}{25^0} + {\cos ^2}{15^0}\\\,\,\,\,\, = \left( {{{\sin }^2}{{15}^0} + {{\cos }^2}{{15}^0}} \right) + \left( {{{\sin }^2}{{25}^0} + {{\cos }^2}25} \right) + \left( {{{\sin }^2}{{35}^0} + {{\cos }^2}{{35}^0}} \right) + {\sin ^2}{45^0}\\\,\,\,\, = 1 + 1 + 1 + {\left( {\dfrac{{\sqrt 2 }}{2}} \right)^2} = 3 + \dfrac{1}{2} = \dfrac{7}{2}.\end{array}\)
Giá trị của biểu thức \(P = {\cos ^2}{20^0} + {\cos ^2}{40^0} + {\cos ^2}{50^0} + {\cos ^2}{70^0}\) bằng
Ta có:
\(\begin{array}{l}P = {\cos ^2}{20^0} + {\cos ^2}{40^0} + {\cos ^2}{50^0} + {\cos ^2}{70^0}\\ = {\cos ^2}{20^0} + {\cos ^2}{40^0} + {\sin ^2}{40^0} + {\sin ^2}{20^0}\\ = \left( {{{\cos }^2}{{20}^0} + {{\sin }^2}{{20}^0}} \right) + \left( {{{\cos }^2}{{40}^0} + {{\sin }^2}{{40}^0}} \right)\\ = 1 + 1 = 2.\end{array}\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 3,AB = 4\). Khi đó \(\cos B\) bằng
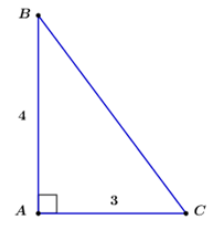
Tam giác \(ABC\) vuông tại \(A\), áp dụng định lí Pi-ta-go ta có:
\(B{C^2} = A{B^2} + A{C^2} = {4^2} + {3^2} = 25 \Rightarrow BC = 5\)
Khi đó \(\cos B = \dfrac{{AB}}{{BC}} = \dfrac{4}{5}\)
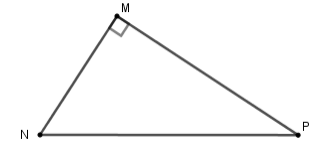
Cho tam giác \(MNP\) vuông tại \(M\). Khi đó \(\tan \widehat {MNP}\) bằng
Ta có \(\tan \widehat {MNP} = \dfrac{{MP}}{{NN}}\)
Khẳng định nào sau đây là đúng? Cho hai góc phụ nhau thì
Với hai góc phụ nhau thì sin góc nọ bằng sin góc kia và tan góc nọ bằng cotan góc kia.
Cho tam giác \(ABC\) vuông tại \(C\) có \(AC = 1\,cm,\,\,BC = 2\,cm.\) Tính các tỉ số lượng giác \(\sin B;\cos B\)
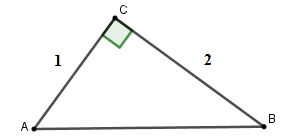
Theo định lý Py-ta-go ta có: \(A{B^2} = A{C^2} + B{C^2} \Rightarrow AB = \sqrt {{1^2} + {2^2}} = \sqrt 5 \)
Xét tam giác \(ABC\) vuông tại \(C\) có \(\sin B = \dfrac{{AC}}{{AB}} = \dfrac{1}{{\sqrt 5 }} = \dfrac{{\sqrt 5 }}{5}\) và \(\cos B = \dfrac{{BC}}{{AB}} = \dfrac{2}{{\sqrt 5 }} = \dfrac{{2\sqrt 5 }}{5}\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 9\,cm,\,\,AC = 5cm.\) Tính tỉ số lượng giác \(\tan C\) (làm tròn đến chữ số thập phân thứ \(1\) )
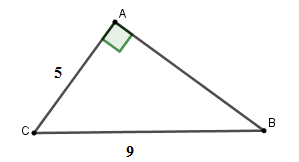
Theo định lý Py-ta-go ta có: \(B{C^2} = A{C^2} + A{B^2} \Rightarrow AB = \sqrt {{9^2} - {5^2}} = 2\sqrt {14} \)
Xét tam giác \(ABC\) vuông tại \(C\) có \(\tan C = \dfrac{{AB}}{{AC}} = \dfrac{{2\sqrt {14} }}{5} \approx 1,5\)
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) có \(AC = 15\,cm,\,CH = 6\,cm\). Tính tỉ số lượng giác \(\cos B\).
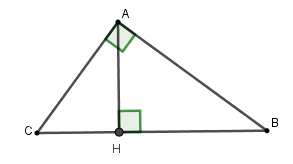
Xét tam giác \(AHC\) vuông tại \(H\), theo định lý Pytago ta có
\(A{H^2} = A{C^2} - C{H^2} = {15^2} - {6^2} = 189 \Rightarrow AH = 3\sqrt {21} \)
\( \Rightarrow \sin C = \dfrac{{AH}}{{AC}} = \dfrac{{3\sqrt {21} }}{{15}} = \dfrac{{\sqrt {21} }}{5}\)
Mà tam giác \(ABC\) vuông tại \(A\) nên \(\widehat B,\widehat C\) là hai góc phụ nhau. Do đó \(\cos B = \sin C = \dfrac{{\sqrt {21} }}{5}.\)
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) có \(CH = 11\,cm,\,BH = 12\,cm.\) Tính tỉ số lượng giác \(\cos C\) (làm tròn đến chữ số thập phân thứ \(2\) )
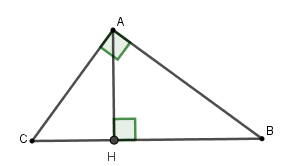
Xét tam giác \(ABC\) vuông tại \(A\) có \(BC = BH + CH = 11 + 12\, = 23\,cm\)
theo hệ thức lượng trong tam giác vuông ta có \(A{C^2} = CH.BC \Rightarrow A{C^2} = 11.23 = 253 \Rightarrow AC = \sqrt {253} \,\,cm\)
\( \Rightarrow \cos C = \dfrac{{AC}}{{BC}} = \dfrac{{\sqrt {253} }}{{23}} \approx 0,69\).
Cho tam giác \(ABC\) vuông tại \(A\). Hãy tính \(\tan C\) biết rằng \(\tan B = 4\).
Vì tam giác \(ABC\) vuông tại \(A\) nên \(\widehat B + \widehat C = 90^\circ \)\( \Rightarrow \cot C = \tan B = 4\)
Mà \(\cot C.\tan C = 1 \Leftrightarrow \tan C = \dfrac{1}{4}.\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 9\,cm,\,\,\tan C = \dfrac{5}{4}\) . Tính độ dài các đoạn thẳng \(AC\) và \(BC\) . (làm tròn đến chữ số thập phân thứ \(2\) )
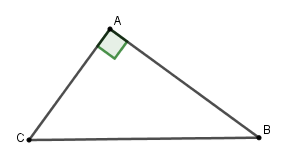
Vì tam giác \(ABC\) vuông tại \(A\) nên \(\tan C = \dfrac{{AB}}{{AC}} \Rightarrow AC = AB:\tan C = 9:\dfrac{5}{4} = 7,2cm\)
Theo định lý Pytago ta có \(B{C^2} = A{B^2} + A{C^2} = {9^2} + 7,{2^2} = 132,84 \Rightarrow BC = \dfrac{{9\sqrt {41} }}{5} \approx 11,53\)
Vậy \(AC = 7,2;BC \approx 11,53.\)
Tính \(\sin \alpha ,\,\,\tan \alpha \) biết \(\cos \alpha = \dfrac{3}{4}\).
Ta có \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\sin ^2}\alpha = 1 - {\cos ^2}\alpha = 1 - \dfrac{9}{{16}} = \dfrac{7}{{16}} \Rightarrow \sin \alpha = \dfrac{{\sqrt 7 }}{4}\)
Lại có \(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }} = \dfrac{{\dfrac{{\sqrt 7 }}{4}}}{{\dfrac{3}{4}}} = \dfrac{{\sqrt 7 }}{3}\).
Vậy \(\sin \alpha = \dfrac{{\sqrt 7 }}{4};\tan \alpha = \dfrac{{\sqrt 7 }}{3}\).
Không dùng bảng số và máy tính, hãy so sánh \(\cot 50^\circ \) và \(\cot 46^\circ \)
Vì \(46^\circ < 50^\circ \Leftrightarrow \cot 46^\circ > \cot 50^\circ \).
Sắp xếp các tỉ số lượng giác \(\sin 40^\circ ,\,\,\cos 67^\circ ,\,\,\sin 35^\circ ,\,\,\cos 44^\circ 35',\,\,\sin 28^\circ 10'\) theo thứ tự tăng dần.
Ta có \(\cos 67^\circ = \sin 23^\circ \,\) vì \(67^\circ + 23^\circ = 90^\circ \); \(\cos 44^\circ 35' = \sin 45^\circ 25'\) vì \(44^\circ 35' + 45^\circ 25' = 90^\circ \)
Mà \(23^\circ < 28^\circ 10' < 35^\circ < 40^\circ < 45^\circ 25'\) nên \(\sin 23^\circ < \sin 28^\circ 10' < \sin 35^\circ < \sin 40^\circ < \sin 45^\circ 25'\)
\( \Leftrightarrow \cos 67^\circ < \sin 28^\circ 10' < \sin 35^\circ < \sin 40^\circ < \cos 44^\circ 35'\)
Tính giá trị biểu thức \({\sin ^2}{10^ \circ } + {\sin ^2}{20^ \circ } + \,\,\,...\,\,\, + {\sin ^2}{70^ \circ } + {\sin ^2}{80^ \circ }\)
Ta có \({\sin ^2}80^\circ = {\cos ^2}10^\circ ;{\sin ^2}70^\circ = {\cos ^2}20^\circ ;{\sin ^2}60^\circ = {\cos ^2}30^\circ ;{\sin ^2}50^\circ = {\cos ^2}40^\circ \) và \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
Nên \({\sin ^2}10^\circ + {\sin ^2}20^\circ + {\sin ^2}30^\circ + {\sin ^2}40^\circ + {\sin ^2}50^\circ + {\sin ^2}60^\circ + {\sin ^2}70^\circ + {\sin ^2}80^\circ \)
\( = {\sin ^2}10^\circ + {\sin ^2}20^\circ + {\sin ^2}30^\circ + {\sin ^2}40^\circ + {\cos ^2}40 + {\cos ^2}30^\circ + {\cos ^2}20^\circ + {\cos ^2}10^\circ \)
\( = \left( {{{\sin }^2}10^\circ + {{\cos }^2}10^\circ } \right) + \left( {{{\sin }^2}20^\circ + {{\cos }^2}20^\circ } \right) + \left( {{{\sin }^2}30^\circ + {{\cos }^2}30^\circ } \right) + \left( {{{\sin }^2}40^\circ + {{\cos }^2}40^\circ } \right)\)
\( = 1 + 1 + 1 + 1 = 4.\)
Vậy giá trị cần tìm là \(4.\)
Tính giá trị biểu thức \(B = \tan 10^\circ .\tan 20^\circ .\tan 30^\circ .....tan80^\circ \)
Ta có \(\tan 80^\circ = cot10^\circ ;\tan 70^\circ = cot20^\circ ;\tan 50^\circ = cot40^\circ ;\tan 60^\circ = \cot 30^\circ \) và \(\tan \alpha .cot\alpha = 1\)
Nên \(B = \tan 10^\circ .\tan 20^\circ .\tan 30^\circ .\tan 40^\circ .\tan 50^\circ .\tan 60^\circ .\tan 70^\circ .tan80^\circ \)\( = \tan 10^\circ .\tan 20^\circ .\tan 30^\circ .\tan 40^\circ .\cot 40^\circ .\cot 30^\circ .\cot 20^\circ .\cot 10^\circ \)
\( = \left( {\tan 10^\circ .\cot 10^\circ } \right).\left( {\tan 20^\circ .\cot 20^\circ } \right).\left( {\tan 30^\circ .\cot 30^\circ } \right).\left( {\tan 40^\circ .\cot 40^\circ } \right)\)
\( = 1.1.1.1 = 1\)
Vậy \(B = 1\).

