Cho hình trụ có chu vi đáy là 8π và chiều cao h=10 . Tính thể tích hình trụ.
Ta có chu vi đáy C=2πR=8π⇒R=4
Thể tích hình trụ là V=πR2h=π.42.10=160π (đvtt).
Cho hình trụ có bán kính đáy R=4(cm) và chiều cao h=5(cm) . Diện tích xung quanh của hình trụ là
Diện tích xung quanh của hình trụ là Sxq=2πRh=2π.4.5=40π(cm2)
Cho hình trụ có bán kính đáy R=8cm và diện tích toàn phần 564πcm2 . Tính chiều cao của hình trụ.
Ta có diện tích toàn phần của hình trụ Stp=Sxq+S2d=2πRh+2πR2=564π
⇔16πh+2π.82=564π⇒h=27,25cm
Cho hình trụ có bán kính đáy R=3(cm) và chiều cao h=6(cm) . Diện tích xung quanh của hình trụ là
Diện tích xung quanh của hình trụ là Sxq=2πRh=2π.3.6=36π(cm2)
Cho hình trụ có chu vi đáy là 10π và chiều cao h=11 . Tính thể tích hình trụ.
Ta có chu vi đáy C=2πR=10π⇒R=5
Thể tích hình trụ là V=πR2h=π.52.11=275π (đvtt).
Cho hình trụ có bán kính đáy R=12cm và diện tích toàn phần 672πcm2 . Tính chiều cao của hình trụ.
Ta có diện tích toàn phần của hình trụ
⇔24πh+2π.122=672π⇒h=16cm
Chọn câu đúng. Cho hình trụ có bán kính đáy R và chiều cao h . Nếu ta giảm chiều cao đi chín lần và tăng bán kính đáy lên ba lần thì
Chiều cao mới của hình trụ là h′=h9 ; bán kính đáy mới là R′=3R
Hình trụ mới có :
Chu vi đáy 2πR′=2π.3R=6πR=3.2πR=3C nên phương án D sai.
Diện tích toàn phần 2πR′h+2πR′2=2π3Rh9+2π.(3R)=2πRh3+6πR≠2πRh+2πR2 nên phương án B sai.
Thể tích πR′2h′=π(3R)2h9=9πR2h9=πR2h nên phương án A đúng.
Diện tích xung quanh 2πR′h′=2π.3R.h9=2πRh3≠2πRh nên phương án C sai.
Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao h=10cm và đường kính đáy là d=6cm . Tính diện tích toàn phần của hộp sữa. Lấy π⋍
Bán kính đường tròn đáy R = \dfrac{6}{2} = 3\,cm nên diện tích một đáy là S_đ=\pi.R^2=9\pi\,(cm^2)
Ta có diện tích xung quanh của hình trụ {S_{xq}} = 2\pi Rh = 2\pi .3.10 = 60\pi \,c{m^2}
Vì hộp sữa đã mất nắp nên diện tích toàn phần của hộp sữa là {S_{tp}} = 9\pi + 60\pi = 69\pi \,\left( {c{m^2}} \right)
Một trục lăn có dạng hình trụ nằm ngang (như hình vẽ), hình trụ có diện tích một đáy S = 36\pi \,c{m^2} và chiều cao h = 8\,cm . Nếu trục lăn đủ 10 vòng thì diện tích tạo trên sân phẳng là bao nhiêu?
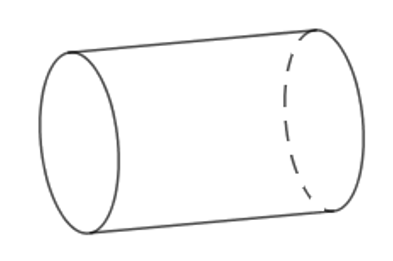
Bán kính R của đường tròn đáy là \pi {R^2} = 36\pi \Rightarrow R = 6\,cm
Diện tích xung quanh của hình trụ {S_{xq}} = 2\pi Rh = 2\pi .6.8 = 96\pi \,\left( {c{m^2}} \right)
Vì trục lăn 10 vòng nên diện tích tạo trên sân phẳng là 10.96\pi = 960\pi \,\left( {c{m^2}} \right)
Cho hình trụ bị cắt bỏ một phần OABB'A'O' như hình vẽ. Thể tích phần còn lại là:
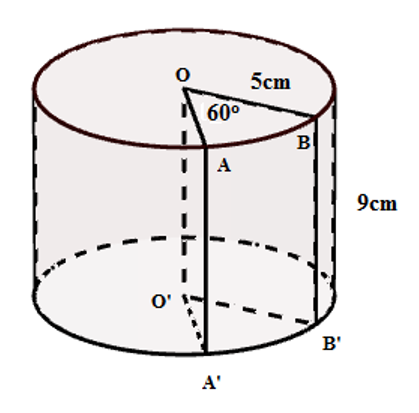
Phần hình trụ bị cắt đi chiếm \dfrac{{60^\circ }}{{360^\circ }} = \dfrac{1}{6} (hình trụ)
Thể tích phần còn lại là V = \dfrac{5}{6}\pi {R^2}h = \dfrac{5}{6}\pi {.5^2}.9 = 187,5\pi \,\,\left( {c{m^3}} \right)
Tính chiều cao của hình trụ có diện tích toàn phần gấp ba lần diện tích xung quanh và bán kính đáy là 4\,cm .
Từ giả thiết ta có 2\pi Rh + 2\pi {R^2} = 3.2.\pi Rh \Rightarrow 2Rh = {R^2} \Rightarrow h = \dfrac{R}{2} = 2cm . Vậy chiều cao của hình trụ là 2\,cm .
Một hình trụ có thể tích 8{m^3} không đổi. Hỏi bán kính đáy bằng bao nhiêu để diện tích toàn phần của hình trụ đó là nhỏ nhất.
Gọi bán kính đáy và chiều cao của hình trụ lần lượt là R,\,\,h\,\,\left( {R > 0;\,h > 0} \right)
Ta có 8 = \pi {R^2}h \Rightarrow h = \dfrac{8}{{\pi {R^2}}}
Diện tích toàn phần của hình trụ {S_{tp}} = 2\pi Rh + 2\pi {R^2} = 2\pi R.\dfrac{8}{{\pi {R^2}}} + 2\pi {R^2} = \dfrac{{16}}{R} + 2\pi {R^2}
= \dfrac{8}{R} + \dfrac{8}{R} + 2\pi {R^2}\mathop \ge \limits_{\cos i} 3\sqrt[3]{{\dfrac{8}{R}.\dfrac{8}{R}.2\pi {R^2}}} = 3\sqrt[3]{{2\pi 64}} = 12\sqrt[3]{{2\pi }}
Dấu “=” xảy ra \Leftrightarrow \dfrac{8}{R} = 2\pi {R^2} \Rightarrow R = \sqrt[3]{{\dfrac{4}{\pi }}}
Vậy với R = \sqrt[3]{{\dfrac{4}{\pi }}} thì {S_{tp}} đạt giá trị nhỏ nhất là 12\sqrt[3]{{2\pi }}.
Cho hình trụ có bán kính đáy R và chiều cao h . Nếu ta tăng chiều cao lên hai lần và giảm bán kính đáy đi hai lần thì
Chiều cao mới của hình trụ là h' = 2h ; bán kính đáy mới là R' = \dfrac{R}{2}
Hình trụ mới có :
Chu vi đáy 2\pi R' = 2\pi \dfrac{R}{2} = \pi R < 2\pi R = C nên phương án D sai.
Diện tích toàn phần 2\pi R'h + 2\pi {R'^2} = 2\pi Rh + \dfrac{{\pi {R^2}}}{2} \ne 2\pi Rh + 2\pi {R^2} nên phương án B sai.
Thể tích \pi {R'^2}h = \dfrac{{\pi {R^2}h}}{4} \ne \pi {R^2}h nên phương án A sai.
Diện tích xung quanh 2\pi R'h = 2\pi .\dfrac{R}{2}.2h = 2\pi Rh nên phương án C đúng.
Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao h = 12cm và đường kính đáy là d= 8\,cm . Tính diện tích toàn phần của hộp sữa. Lấy \pi \simeq 3,14
Bán kính đường tròn đáy R = \dfrac{8}{2} = 4\,cm nên diện tích một đáy {S_d} = \pi {R^2} = 16\pi \,(c{m^2})
Ta có diện tích xung quanh của hình trụ {S_{xq}} = 2\pi Rh = 2\pi .4.12 = 96\pi \,(c{m^2})
Vì hộp sữa đã mất nắp nên diện tích xung quanh của hộp sữa {S_{tp}} = 96\pi + 16\pi = 112\pi \,\left( {c{m^2}} \right).
Một trục lăn có dạng hình trụ nằm ngang (như hình vẽ), hình trụ có diện tích một đáy S = 25\pi \,c{m^2} và chiều cao h = 10\,cm . Nếu trục lăn đủ 12 vòng thì diện tích tạo trên sân phẳng là bao nhiêu?
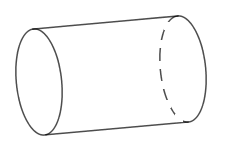
Bán kính R của đường tròn đáy là \pi {R^2} = 25\pi \Rightarrow R = 5\,cm
Diện tích xung quanh của hình trụ
{S_{xq}} = 2\pi Rh = 2\pi .5.10 = 100\pi \left( {c{m^2}} \right)
Vì trục lăn 12 vòng nên diện tích tạo trên sân phẳng là 12.100\pi = 1200\pi \,\left( {c{m^2}} \right)
Biết BC = 25cm và AH = 12cm. Hãy tính diện tích xung quanh của hình tạo thành bởi khi cho tứ giác ADHE quay quanh AD.
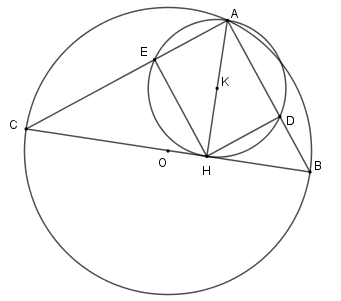
Xét tam giác vuông ABC có HB.HC = A{H^2} \Leftrightarrow HB.HC = 144 và HB + HC = BC \Leftrightarrow HB + HC = 25
Suy ra HB = 9\,cm;\,HC = 16\,cm (Chú ý: AB < AC nên HB < HC).
Xét tam giác vuông AHB có \dfrac{1}{{H{D^2}}} = \dfrac{1}{{A{H^2}}} + \dfrac{1}{{H{B^2}}} \Rightarrow HD = \dfrac{{36}}{5}\,cm
Tương tự ta có HE = \dfrac{{48}}{5}cm \Rightarrow AD = \dfrac{{48}}{5}\,cm.
Khi quay hình chữ nhật ADHE quanh AD ta được hình trụ có chiều cao AD và bán kính đáy HD.
Nên {S_{xq}} = 2.\pi HD.AD = \dfrac{{3456}}{{25}}\pi \left( {c{m^2}} \right)
Chọn khẳng định sai.
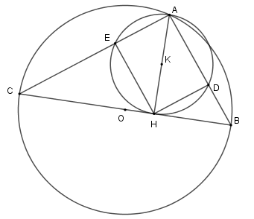
Xét \left( O \right) có \widehat {CAD} = 90^\circ (góc nội tiếp chắn nửa đường tròn)
Xét \left( K \right) có \widehat {AEH} = \widehat {ADH} = 90^\circ (góc nội tiếp chắn nửa đường tròn)
Nên tứ giác ADHE là hình chữ nhật ( vì có ba góc vuông) \Rightarrow phương án A đúng.
Xét tam giác vuông AHB có A{H^2} = AD.AB \Rightarrow phương án C đúng
Xét tam giác vuông A{H^2} = AC.AE nên AD.AB = AC.AE \Rightarrow phương án B đúng
Chọn khẳng định sai.

Xét \left( O \right) có \widehat {CAD} = 90^\circ (góc nội tiếp chắn nửa đường tròn)
Xét \left( K \right) có \widehat {AEH} = \widehat {ADH} = 90^\circ (góc nội tiếp chắn nửa đường tròn)
Nên tứ giác ADHE là hình chữ nhật ( vì có ba góc vuông) \Rightarrow phương án A đúng.
Xét tam giác vuông AHB có A{H^2} = AD.AB \Rightarrow phương án C đúng
Xét tam giác vuông A{H^2} = AC.AE nên AD.AB = AC.AE \Rightarrow phương án B đúng
Chọn khẳng định sai.

Xét \left( O \right) có \widehat {CAD} = 90^\circ (góc nội tiếp chắn nửa đường tròn)
Xét \left( K \right) có \widehat {AEH} = \widehat {ADH} = 90^\circ (góc nội tiếp chắn nửa đường tròn)
Nên tứ giác ADHE là hình chữ nhật ( vì có ba góc vuông) \Rightarrow phương án A đúng.
Xét tam giác vuông AHB có A{H^2} = AD.AB \Rightarrow phương án C đúng
Xét tam giác vuông A{H^2} = AC.AE nên AD.AB = AC.AE \Rightarrow phương án B đúng
Tính chiều cao của hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh và bán kính đáy là 3\,cm .
Từ giả thiết ta có 2\pi Rh + 2\pi {R^2} = 2.2.\pi Rh \Rightarrow Rh = {R^2} \Rightarrow R = h . Vậy chiều cao của hình trụ là3\,cm .

