Bài tập ôn tập chương 2

Vì đường thẳng \(AB\) đi qua \(A\left( { - 1;2} \right)\) nên gọi phương trình đường thẳng \(AB\)có hệ số góc \(k\):

\(y = k\left( {x + 1} \right) + 2.\)

Mà \(AB \bot \left( \Delta  \right) = B\) nên suy ra: \(k.\left( { - 4} \right) =  - 1\, \Rightarrow k = \dfrac{1}{4}\)

Khi đó phương trình đường thẳng \(AB\) là: \(y = \dfrac{1}{4}\left( {x + 1} \right) + 2\) hay \(y = \dfrac{1}{4}x + \dfrac{9}{4}.\)

Khi đó tọa độ điểm \(B\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}y = \dfrac{1}{4}x + \dfrac{9}{4}\\y =  - 4x + 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x =  - \dfrac{5}{{17}}\\y = \dfrac{{37}}{{17}}\end{array} \right. \Rightarrow B\left( {\dfrac{{ - 5}}{{17}};\dfrac{{37}}{{17}}} \right)\)

Vậy \(B\left( {\dfrac{{ - 5}}{{17}};\dfrac{{37}}{{17}}} \right).\)

Ta có:

\(\begin{array}{l}y = \left( {m - 2} \right)x + m\\ \Leftrightarrow y = mx - 2x + m\\ \Leftrightarrow \left( {x + 1} \right)m - 2x - y = 0\,\,\,\left( * \right)\end{array}\)

Để phương trình (*) nghiệm đúng với mọi \(m\) thì \(\left\{ \begin{array}{l}x + 1 = 0\\ - 2x - y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 1\\y = 2\end{array} \right.\).

Vậy đường thẳng \(\left( d \right)\) luôn đi qua \(A\left( { - 1;2} \right)\) với mọi \(m\).

Để \(\left( d \right)\) song song với \(\left( \Delta  \right)\) thì: \(\left\{ \begin{array}{l}m - 2 =  - 4\\m \ne 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}m =  - 2\\m \ne 1\end{array} \right. \Rightarrow m =  - 2.\)

Vậy \(m =  - 2\) thỏa mãn yêu cầu.

Để \(\left( d \right)\) song song với \(\left( \Delta  \right)\) thì: \(\left\{ \begin{array}{l}m - 2 =  - 4\\m \ne 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}m =  - 2\\m \ne 1\end{array} \right. \Rightarrow m =  - 2.\)

Vậy \(m =  - 2\) thỏa mãn yêu cầu.

Điều kiện: \(m \ne 0.\)

+) Với \(y = 0 \Rightarrow mx - 2 = 0 \Rightarrow mx = 2 \Rightarrow x = \dfrac{2}{m}\)

\( \Rightarrow \left( {{d_m}} \right):y = mx - 2\) với  cắt \(Ox\) tại điểm \(A\left( {\dfrac{2}{m};\,\,0} \right).\)

+) Với \(x = 0 \Rightarrow y =  - 2 \Rightarrow B\left( {0;\,\, - 2} \right)\) là giao của \(\left( {{d_m}} \right)\) và \(Oy.\)

Khi đó diện tích của tam giác sẽ là:

\(\begin{array}{l}{S_{OAB}} = \dfrac{1}{2}OA.OB = \dfrac{1}{2}.\left| {\dfrac{2}{m}} \right|.\left| { - 2} \right| = \dfrac{2}{{\left| m \right|}} = 1\\ \Leftrightarrow \left| m \right| = 2 \Leftrightarrow \left[ \begin{array}{l}m = 2\\m =  - 2\end{array} \right..\end{array}\)

Vậy \(m = 2\) hoặc \(m =  - 2\) thì đường thẳng \(\left( {{d_m}} \right)\) cắt hai trục tọa độ tạo thành tam giác có diện tích bằng 1.

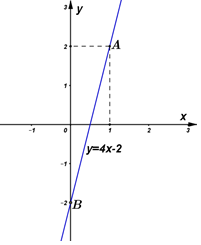
Đường thẳng \(\left( {{d_m}} \right)\) đi qua điểm \(A\left( {1;2} \right)\) nên ta thay tọa độ điểm \(A\)  vào phương trình đường thẳng  \(\left( {{d_m}} \right)\) ta được:  \(2 = m.1 - 2 \Rightarrow m = 4\)

Khi \(m = 4\) đường thẳng có phương trình \(y = 4x - 2\)

Hàm số \(y = mx - 2\) đồng biến\( \Leftrightarrow m > 0\)

Vậy \(m > 0.\)

Chọn A.

Hàm số \(y = mx - 2\) đồng biến\( \Leftrightarrow m > 0\)

Vậy \(m > 0.\)

Chọn A.

Hai đường thẳng \({d_1}\) và \({d_2}\) cùng đi qua điểm \(A\left( {1;0} \right)\) nên ta thay tọa độ điểm A vào hai phương trình ta được:

\(\left\{ \begin{array}{l}0 = \left( {m - 2} \right).1 + m + 4\\0 = \left( {n + 1} \right).1 - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m - 2 + m + 4 = 0\\n + 1 - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m =  - 2\\n = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m =  - 1\\n = 2\end{array} \right.\)

Vậy \(m =  - 1;n = 2\).

Hàm số có đồ thị \({d_1}:y = \left( {m - 2} \right)x + m + 4\) luôn nghịch biến \( \Leftrightarrow m - 2 < 0 \Leftrightarrow m < 2\)

Hàm số có đồ thị \({d_2}:y = \left( {n + 1} \right)x - 3\) luôn đồng biến \( \Leftrightarrow n + 1 > 0 \Rightarrow n >  - 1\)

Vậy \(m < 2\) thì hàm số có đồ thị \({d_1}\) luôn nghịch biến.

       \(n >  - 1\) thì hàm số có đồ thị \({d_2}\) luôn đồng biến.

Hàm số có đồ thị \({d_1}:y = \left( {m - 2} \right)x + m + 4\) luôn nghịch biến \( \Leftrightarrow m - 2 < 0 \Leftrightarrow m < 2\)

Hàm số có đồ thị \({d_2}:y = \left( {n + 1} \right)x - 3\) luôn đồng biến \( \Leftrightarrow n + 1 > 0 \Rightarrow n >  - 1\)

Vậy \(m < 2\) thì hàm số có đồ thị \({d_1}\) luôn nghịch biến.

       \(n >  - 1\) thì hàm số có đồ thị \({d_2}\) luôn đồng biến.

Đồ thị hàm số $y = {\rm{ax}} + b$ cắt trục hoành $ \Rightarrow y = 0 \Rightarrow {\rm{ax}} + b = 0 \Leftrightarrow x =  - \dfrac{b}{a}$

ĐTHS $y = {\rm{ax}} + b$ cắt trục tung $ \Rightarrow x = 0 \Rightarrow y = {\rm{a}}{\rm{.0}} + b \Rightarrow y = b$

Vậy đồ thị hàm số $y = {\rm{ax}} + b\,(a \ne 0)$ cắt trục hoành tại điểm có hoành độ bằng $-\dfrac{b}{a}$ và cắt trục tung tại điểm có tung độ bằng $b$.

Đáp án A: Thay $ x_0=0;y_0=1$ vào hàm số, ta có $ 2.0 + 1 = 1  \Rightarrow (0;1)$ thuộc ĐTHS đã cho.

Điểm $(1;2)$ thuộc ĐTHS $x - y = m \Leftrightarrow 1 - 2 = m \Leftrightarrow  - 1 = m$.

Ta có $3( - 2) - 2.3 =  - 12 \ne 3$=> loại A

$3( - 2) - 3 =  - 9 \ne 0$ => loại B

$0( - 2) + 3 = 3$

Ta có điểm $O\left( {0\;;0} \right)$ thuộc đường thẳng $y = (3 - m)x + m + 3 \Leftrightarrow (3-m).0+m + 3 = 0  $$\Leftrightarrow m+3=0\Leftrightarrow m =  - 3$

Xét phương trình hoành độ giao điểm $A$ của $\left( {d'} \right)$  và $\left( {d''} \right)$:

$\begin{array}{*{20}{l}}{2x + 4 =  - 3x - 1}\\{ \Leftrightarrow 5x =  - 5}\\{ \Leftrightarrow x =  - 1}\\{ \Rightarrow y = 2\left( { - 1} \right) + 4 = 2}\\{ \Rightarrow A\left( { - 1;2} \right)}\end{array}$

Để $\left( d \right);\left( {d'} \right);\left( {d''} \right)$ đồng quy thì $A\left( { - 1;2} \right) \in \left( d \right)$

$\begin{array}{*{20}{l}}{ \Leftrightarrow 2 = \left( {m + 2} \right).\left( { - 1} \right) - 3m}\\{ \Leftrightarrow 2 =  - 2 - 4m}\\{ \Leftrightarrow 4m =  - 4}\\{ \Leftrightarrow m =  - 1}\end{array}$

Vậy khi $m =  - 1$ thì $\left( d \right);\left( {d'} \right);\left( {d''} \right)$  đồng quy tại $A\left( { - 1;2} \right)$.

Gọi $d:y = {\rm{ax}} + b$ là đường thẳng đi qua $A$ và $B$.

$\begin{array}{l}A(0;3) \in d \Leftrightarrow a.0 + b = 3 \Leftrightarrow b = 3\\B(2;2) \in d \Leftrightarrow a.2 + b = 2\\ \Rightarrow \left\{ \begin{array}{l}b = 3\\2a + b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 3\\a =  - \dfrac{1}{2}\end{array} \right. \Rightarrow d:y =  - \dfrac{1}{2}x + 3\end{array}$

Để $3$  điểm $A,B,C$ thẳng hàng thì $C(m + 3;m) \in (d):y =  - \dfrac{1}{2}x + 3$

$ \Leftrightarrow m =  - \dfrac{1}{2}\left( {m + 3} \right) + 3 \Leftrightarrow \dfrac{3}{2}m = \dfrac{3}{2} \Leftrightarrow m = 1$.

Vậy $m = 1$.

$d:y = x + 3;d':y =  - x + 1;d'':y = \sqrt 3 x - m - 2$

Xét phương trình hoành độ giao điểm của $d$ và $d'$: $x + 3 =  - x + 1 \Leftrightarrow 2x =  - 2 \Leftrightarrow x =  - 1 \Rightarrow y = 2$

Do đó $d$ và $d'$ cắt nhau tại điểm $\left( { - 1;2} \right)$.

Điểm $A( - 1;2) \in d'':y = \sqrt 3 x - m - 2 $$\Leftrightarrow 2 = \sqrt 3 .\left( { - 1} \right) - m - 2 $$\Leftrightarrow m =  - 4 - \sqrt 3 $

Vậy $m =  - 4 - \sqrt 3 $.

Đồ thị hàm số $y = (m - 1)x - m$ cắt trục tung tại điểm có tung độ là $1 + \sqrt 2 $

$ \Rightarrow  - m = 1 + \sqrt 2  \Rightarrow m =  - 1 - \sqrt 2 $