Góc có đỉnh bên ngoài đường tròn có số đo
Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
Góc có đỉnh bên trong đường tròn có số đo
Số đo của góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Cho đường tròn (O) và điểm E nằm ngoài đường tròn. Vẽ cát tuyến EAB và ECD với đường tròn (A nằm giữa E và B, C nằm giữa E và D). Gọi F là một điểm trên đường tròn sao cho B nằm chính giữa cung DF, I là giao điểm của FA và BC. Biết $\widehat E = {25^0}$, số đo góc $\widehat {AIC}$ là:
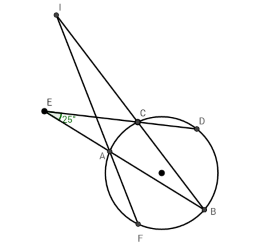
B nằm chính giữa cung $DF$ nên sđ $\overparen {BD}$ = sđ$\overparen {BF}$
Mặt khác góc tại E và I là hai góc có đỉnh bên ngoài đường tròn nên
$\begin{array}{l}\widehat E = \dfrac{1}{2}\left( {sđ\overparen {BD} - sđ \overparen{AC}} \right)\\ = \dfrac{1}{2}\left( {sđ\overparen {BF} - sđ\overparen {AC}} \right) = \widehat I\end{array}$
Theo đề bài ta có
$\widehat E = \widehat I = {25^0}$
Trên \(\left( O \right)\) lấy bốn điểm \(A,B,C,D\) theo thứ tự sao cho cung \(AB = \) cung \(BC = \) cung \(CD\) . Gọi \(I\) là giao điểm của \(BD\) và \(AC\) , biết \(\widehat {BIC} = 80^\circ \) . Tính \(\widehat {ACD}\) .
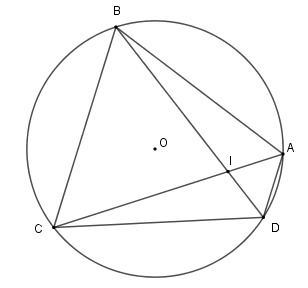
Vì cung \(AB = \) cung \(BC = \) cung \(CD\) nên gọi số đo mỗi cung là $a$ độ. Ta có số đo cung \(AD\) là \(360^\circ - 3a\)
Vì \(\widehat {BIC}\) là góc có đỉnh bên trong đường tròn nên
$\widehat {BIC} = \dfrac{{a + 360^\circ - 3a}}{2} = 80^\circ \Rightarrow a = 100^\circ \Rightarrow $ số đo cung \(AD\) là $360^\circ - 3.100^\circ = 60^\circ $
\(\widehat {ACD}\) là góc nội tiếp chắn cung \(AD\) nên \(\widehat {ACD} = \dfrac{{60^\circ }}{2} = 30^\circ \) .
Cho \(\left( {O;R} \right)\) và dây \(AB\) bất kỳ. Gọi \(M\) là điểm chính giữa cung nhỏ \(AB\) , \(E;F\) là hai điểm bất kỳ trên dây \(AB\) . Gọi \(C,D\) lần lượt là giao điểm của \(ME;MF\) với \(\left( O \right)\) . Khi đó \(\widehat {CEF} + \widehat {CDF}\) bằng
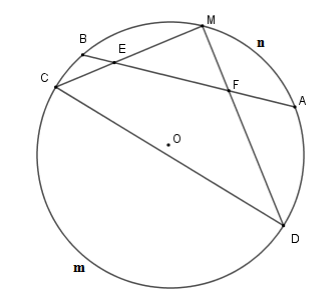
Ta có \(\widehat {CEF}\) là góc có đỉnh bên trong đường tròn nên \(\widehat {CEF} = \dfrac{1}{2}\)(sđ \(\overparen{AmC} + \) sđ \(\overparen{BM}\) )
Và \(\widehat {MDC} = \dfrac{1}{2}\) sđ\(\overparen{MC}\) (góc nội tiếp chắn cung \(MC\))
Từ đó \(\widehat {CEF} + \widehat {CDF} = \dfrac{1}{2}\) (sđ\(\overparen{AmC} + \) sđ \(\overparen{BM}\)$ + $ sđ \(\overparen{MC})\)
Mà cung $AnM = $ cung \(MB\) nên \(\widehat {EFD} + \widehat {ECD} \)
\(= \dfrac{1}{2}\) (sđ\(\overparen{AmC} + \) sđ \(\overparen{AnM}\)$ + $ sđ \(\overparen{MC}\)) =$\dfrac{1}{2}.360^\circ = 180^\circ .$
Tính diện tích tam giác \(CON\) theo \(R\)
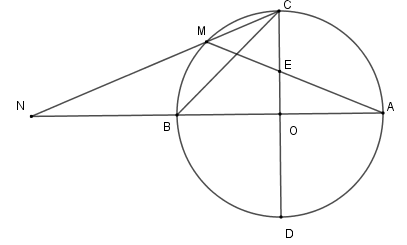
Xét \(\left( O \right)\) có \(\widehat {CNA}\) là góc có đỉnh bên ngoài đường tròn nên \(\widehat {CNB} = \dfrac{1}{2}\) (số đo cung \(AC - \) số đo cung \(MB\) )
Mà số đo cung \(MB = \dfrac{1}{2}\) số đo cung \(AC\) nên \(\widehat {CNA} = \dfrac{1}{2}\)số đo cung \(MB\) .
Lại có \(\widehat {MCB} = \dfrac{1}{2}\) số đo cung \(MB\) (góc nội tiếp) nên \(\widehat {MCB} = \widehat {BNC} \Rightarrow \Delta BNC\) cân tại \(B \Rightarrow BN = BC\)
Xét \(\Delta COB\) vuông cân tại \(O\) ta có \(BC = \sqrt {O{C^2} + O{B^2}} = R\sqrt 2 \) nên \(BN = R\sqrt 2 \)
Suy ra \(NO = NB + OB = R + \sqrt 2 R = R\left( {1 + \sqrt 2 } \right)\)
Khi đó \({S_{ONC}} = \dfrac{1}{2}NO.CO = \dfrac{1}{2}.\left( {1 + \sqrt 2 } \right)R.R = \dfrac{{\sqrt 2 + 1}}{2}{R^2}\) .
Số đo góc \(CNA\) bằng
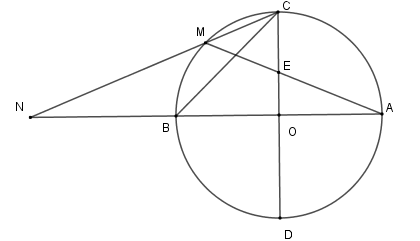
Xét \(\left( O \right)\) có \(\widehat {CNA}\) là góc có đỉnh bên ngoài đường tròn nên \(\widehat {CNB} = \dfrac{1}{2}\) (số đo cung \(AC - \) số đo cung \(MB\) )
\( = \dfrac{1}{2}\left( {90^\circ - 45^\circ } \right) = 22,5^\circ \)
Số đo góc \(MEC\) bằng
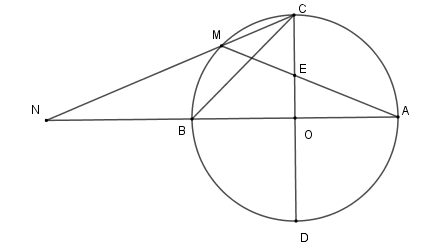
Vì hai đường kính \(AB\) và \(CD\) vuông góc với nhau nên sđ\(\overparen{AC} = \) sđ\(\overparen{AD} = sđ\overparen{BD} = sđ\overparen{BC} = \dfrac{{360^\circ }}{4} = 90^\circ \)
Vì \(M\) là điểm chính giữa cung \(BC\) nên \(sđ\overparen{MC} = sđ\overparen{MB} = \dfrac{{90^\circ }}{2} = 45^\circ \)
Xét \(\left( O \right)\) có \(\widehat {MEC}\) là góc có đỉnh bên trong đường tròn nên \(\widehat {MEC} = \dfrac{1}{2}\) (số đo cung \(AD + \) số đo cung \(MC\) )
\( = \dfrac{{90^\circ + 45^\circ }}{2} = 67,5^\circ \)
Số đo góc \(MEC\) bằng

Vì hai đường kính \(AB\) và \(CD\) vuông góc với nhau nên sđ\(\overparen{AC} = \) sđ\(\overparen{AD} = sđ\overparen{BD} = sđ\overparen{BC} = \dfrac{{360^\circ }}{4} = 90^\circ \)
Vì \(M\) là điểm chính giữa cung \(BC\) nên \(sđ\overparen{MC} = sđ\overparen{MB} = \dfrac{{90^\circ }}{2} = 45^\circ \)
Xét \(\left( O \right)\) có \(\widehat {MEC}\) là góc có đỉnh bên trong đường tròn nên \(\widehat {MEC} = \dfrac{1}{2}\) (số đo cung \(AD + \) số đo cung \(MC\) )
\( = \dfrac{{90^\circ + 45^\circ }}{2} = 67,5^\circ \)
Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) . Các tiếp tuyến tại \(B,C\) của \(\left( O \right)\) cắt nhau tại \(M\) . Biết \(3\widehat {BAC} = \widehat {BMC}\) . Tính \(\widehat {BAC}\) .
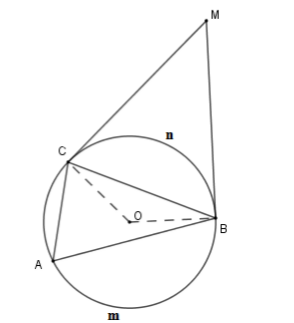
Xét \(\left( O \right)\) có \(\widehat {BMC} = \dfrac{1}{2}\) (số đo cung \(BmC - \) số đo cung \(BnC\) ) (góc có đỉnh bên ngoài đường tròn)
Và \(\widehat {BAC} = \dfrac{1}{2}\) Số đo cung \(BnC\)
Mà \(3\widehat {BAC} = \widehat {BMC}\) nên \(\dfrac{1}{2}\) (sđ \(BmC - \) sđ\(BnC\) )\( = \dfrac{3}{2}\) sđ\(BnC\)
\( \Rightarrow \) số đo cung \(BmC = 4\). Số đo cung \(BnC\) mà số đo cung \(BmC + \) số đo cung \(BnC\)$ = 360^\circ $
Nên số đo cung \(BnC\) là \(\dfrac{{360^\circ }}{5} = 72^\circ \) , do đó \(\widehat {BAC} = \dfrac{{72^\circ }}{2} = 36^\circ \) .
Cho \(\left( {O;R} \right)\) có hai đường kính \(AB,CD\) vuông góc với nhau. Trên đường kính \(AB\) lấy điểm \(E\) sao cho \(AE = R\sqrt 2 \) . Vẽ dây \(CF\) đi qua \(E\) . Tiếp tuyến của đường tròn tại \(F\) cắt đường thẳng \(CD\) tại \(M\) , dây \(AF\) cắt \(CD\) tại \(N\) . Tính độ dài \(ON\) theo \(R.\)
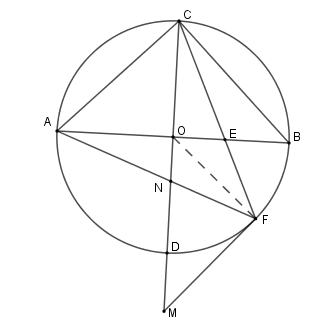
Xét \(\Delta AOC\) vuông cân tại \(O\) có \(AC = \sqrt {O{A^2} + O{C^2}} = R\sqrt 2 \Rightarrow AO = AE\) nên \(\Delta AEC\) cân tại \(A \Rightarrow \widehat {ACE} = \widehat {AEC}\)
Hay \(\dfrac{1}{2}\) (số đo cung \(AD + \) số đo cung \(DF\) ) \( = \dfrac{1}{2}\) (số đo cung \(AC + \) số đo cung \(BF\) ) mà cung \(AD = \) cung \(AC\)
Nên cung \(DF\) \( = \) cung \(BF\).
Lại có cung \(DF\)\( = \) cung \(BF\) nên \(\widehat {NOF} = \widehat {EOF} \Rightarrow \widehat {AOF} = \widehat {COF}\)
Suy ra \(\Delta OAF = \Delta OCF\left( {c - g - c} \right) \Rightarrow \widehat {OFE} = \widehat {OFN}\)
Suy ra \(\Delta OEF = \Delta ONF\left( {g - c - g} \right) \Rightarrow ON = OE = \left( {\sqrt 2 - 1} \right)R\)
Cho tam giác ABC cân tại A, nội tiếp trong (O). Trên cung nhỏ AC, lấy điểm D. Gọi S là giao điểm của AD và BC, I là giao điểm của AC và BD. Khẳng định nào sau đây là đúng?
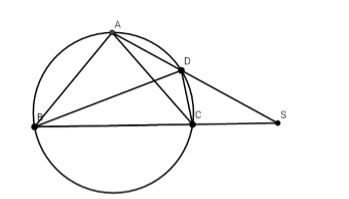
Ta có $\widehat {{\rm{AS}}C}$ là góc có đỉnh nằm ngoài đường tròn nên
$\widehat {{\rm{AS}}C}$=$\dfrac{1}{2}\left( {sđ\overparen{AB} - sđ\overparen{CD}} \right)$
$ = \dfrac{1}{2}\left( {sđ\overparen{AC} - sđ\overparen{CD}} \right)$$ = \dfrac{1}{2}sđ\overparen{AD}$
$ = \widehat {ABD} = \widehat {DCA}$
Tính diện tích tam giác \(CBN\) theo \(R\)
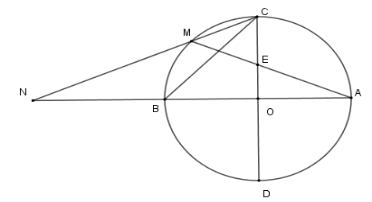
Xét \(\Delta COB\) vuông cân tại \(O\) ta có
\(BC = \sqrt {O{C^2} + O{B^2}} = R\sqrt 2 \)
nên \(BN = R\sqrt 2 \)
Khi đó \({S_{BNC}} = \dfrac{1}{2}NB.CO = \dfrac{{{R^2}\sqrt 2 }}{2}\) .
Hai đoạn thẳng nào sau đây bằng nhau?
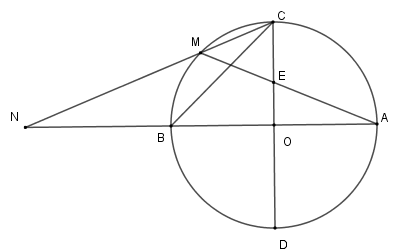
Xét \(\left( O \right)\) có \(\widehat {CNA}\) là góc có đỉnh bên ngoài đường tròn nên
\(\widehat {CNB} = \dfrac{1}{2}\) $ (sđ \overparen{AC}-sđ \overparen{MB})$
Mà sđ $\overparen{MB}$\( = \dfrac{1}{2}\) sđ $\overparen{AC}$ nên \(\widehat {CNA} = \dfrac{1}{2}\)sđ $\overparen{MB}$
Lại có \(\widehat {MCB} = \dfrac{1}{2}\) sđ $\overparen{MB}$ (góc nội tiếp) nên \(\widehat {MCB} = \widehat {BNC} \Rightarrow \Delta BNC\) cân tại \(B \Rightarrow BN = BC\) .
Tam giác \(MCE\) là tam giác gì?
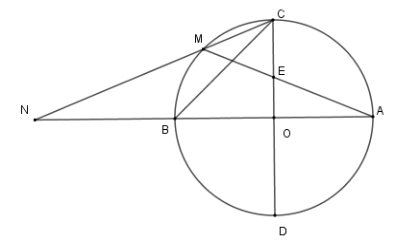
Xét \(\left( O \right)\) có \(\widehat {MEC}\) là góc có đỉnh bên trong đường tròn nên
\(\widehat {MEC} = \dfrac{1}{2}\) (sđ \(\overparen{AD} + \) sđ \(\overparen{MC}\) )
Và \(\widehat {MCE} = \widehat {MCD} \)
\(= \dfrac{1}{2}\) (sđ \(\overparen{BD} + \) sđ \(\overparen{BM}\) )
mà cung \(MB = \) cung \(MC\)
và cung \(AD = \) cung \(BD\)
Từ đó \(\widehat {MEC} = \widehat {MCE} \Rightarrow \Delta MEC\) cân tại \(M\) .
Tam giác \(MCE\) là tam giác gì?

Xét \(\left( O \right)\) có \(\widehat {MEC}\) là góc có đỉnh bên trong đường tròn nên
\(\widehat {MEC} = \dfrac{1}{2}\) (sđ \(\overparen{AD} + \) sđ \(\overparen{MC}\) )
Và \(\widehat {MCE} = \widehat {MCD} \)
\(= \dfrac{1}{2}\) (sđ \(\overparen{BD} + \) sđ \(\overparen{BM}\) )
mà cung \(MB = \) cung \(MC\)
và cung \(AD = \) cung \(BD\)
Từ đó \(\widehat {MEC} = \widehat {MCE} \Rightarrow \Delta MEC\) cân tại \(M\) .
Tích $FE.FB$ bằng
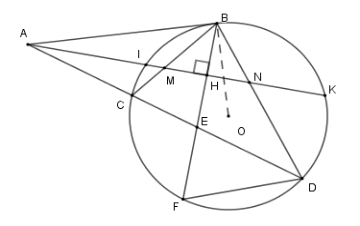
Vì tam giác \(BMN\) cân tại \(B\) có \(BH\) là đường cao nên \(BH\) cũng là đường phân giác.
\( \Rightarrow \widehat {CBF} = \widehat {DBF}\)
\(\Rightarrow \) cung $CF = $ cung \(DF\)
\( \Rightarrow \widehat {DBF} = \widehat {CDF}\) (hệ quả góc nội tiếp)
\( \Rightarrow \Delta FED\backsim\Delta FDB\left( {g - g} \right)\)
\(\Rightarrow \dfrac{{EF}}{{FD}} = \dfrac{{FD}}{{FB}} \Rightarrow FE.FB = F{D^2}\) .
Tam giác \(BMN\) là tam giác gì?
Xét \(\left( O \right)\) có đường thẳng \(AM\) cắt đường tròn tại \(I;K\) .
Khi đó
\(\widehat {BAK} = \dfrac{1}{2}\) (sđ \(\overparen{BK} - \) sđ \(\overparen{BI}\) );
\(\widehat {CAK} = \dfrac{1}{2}\) (sđ \(\overparen{DK} - \) sđ \(\overparen{CI}\) )
Mà \(\widehat {BAK} = \widehat {CAK} \)
\(\Rightarrow \) \(\dfrac{1}{2}\) (sđ \(\overparen{BK}- \) sđ \(\overparen{BI}\) )
\( = \dfrac{1}{2}\) (sđ \(\overparen{DK} - \) sđ \(\overparen{CI}\) )
Nên \( \dfrac{1}{2}\) (sđ \(\overparen{BK} + \) sđ \(\overparen{CI}\) )
\(=\dfrac{1}{2}\) (sđ \(\overparen{DK} + \) sđ \(\overparen{BI}\) )
Hay \(\widehat {BMN} = \widehat {BNM}\)
\(\Rightarrow \Delta BMN\) cân tại \(B\) .
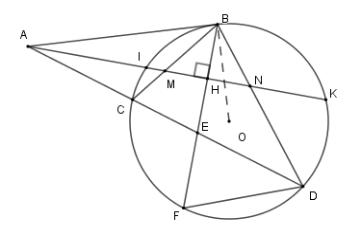
Tam giác \(BMN\) là tam giác gì?

Xét \(\left( O \right)\) có đường thẳng \(AM\) cắt đường tròn tại \(I;K\) .
Khi đó
\(\widehat {BAK} = \dfrac{1}{2}\) (sđ \(\overparen{BK} - \) sđ \(\overparen{BI}\) );
\(\widehat {CAK} = \dfrac{1}{2}\) (sđ \(\overparen{DK} - \) sđ \(\overparen{CI}\) )
Mà \(\widehat {BAK} = \widehat {CAK} \)
\(\Rightarrow \) \(\dfrac{1}{2}\) (sđ \(\overparen{BK}- \) sđ \(\overparen{BI}\) )
\( = \dfrac{1}{2}\) (sđ \(\overparen{DK} - \) sđ \(\overparen{CI}\) )
Nên \( \dfrac{1}{2}\) (sđ \(\overparen{BK} + \) sđ \(\overparen{CI}\) )
\(=\dfrac{1}{2}\) (sđ \(\overparen{DK} + \) sđ \(\overparen{BI}\) )
Hay \(\widehat {BMN} = \widehat {BNM}\)
\(\Rightarrow \Delta BMN\) cân tại \(B\) .
$BC$ là tia phân giác của góc nào dưới đây?
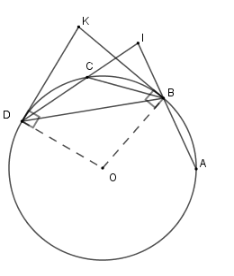
Xét \(\left( O \right)\) có \(\widehat {KBC} = \widehat {CDB}\) (hệ quả góc tạo bởi tiếp tuyến và dây cung)
Lại có \(\widehat {CDB} = \widehat {CBD}\) (hai góc nội tiếp chắn hai cung bằng nhau)
Nên \(\widehat {CBD} = \widehat {KBC} \Rightarrow BC\) là tia phân giác góc \(KBD\) .

