Trả lời bởi giáo viên
Đáp án đúng: d
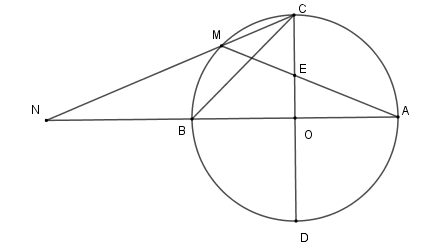
Vì hai đường kính \(AB\) và \(CD\) vuông góc với nhau nên sđ\(\overparen{AC} = \) sđ\(\overparen{AD} = sđ\overparen{BD} = sđ\overparen{BC} = \dfrac{{360^\circ }}{4} = 90^\circ \)
Vì \(M\) là điểm chính giữa cung \(BC\) nên \(sđ\overparen{MC} = sđ\overparen{MB} = \dfrac{{90^\circ }}{2} = 45^\circ \)
Xét \(\left( O \right)\) có \(\widehat {MEC}\) là góc có đỉnh bên trong đường tròn nên \(\widehat {MEC} = \dfrac{1}{2}\) (số đo cung \(AD + \) số đo cung \(MC\) )
\( = \dfrac{{90^\circ + 45^\circ }}{2} = 67,5^\circ \)
Hướng dẫn giải:
Sử dụng: Góc có đỉnh bên trong đường tròn có số đo bằng nửa tổng số đo hai cung bị chắn.
