Câu hỏi:
2 năm trước
Trên \(\left( O \right)\) lấy bốn điểm \(A,B,C,D\) theo thứ tự sao cho cung \(AB = \) cung \(BC = \) cung \(CD\) . Gọi \(I\) là giao điểm của \(BD\) và \(AC\) , biết \(\widehat {BIC} = 80^\circ \) . Tính \(\widehat {ACD}\) .
Trả lời bởi giáo viên
Đáp án đúng: d
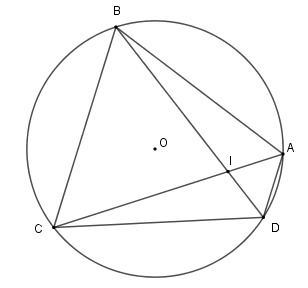
Vì cung \(AB = \) cung \(BC = \) cung \(CD\) nên gọi số đo mỗi cung là $a$ độ. Ta có số đo cung \(AD\) là \(360^\circ - 3a\)
Vì \(\widehat {BIC}\) là góc có đỉnh bên trong đường tròn nên
$\widehat {BIC} = \dfrac{{a + 360^\circ - 3a}}{2} = 80^\circ \Rightarrow a = 100^\circ \Rightarrow $ số đo cung \(AD\) là $360^\circ - 3.100^\circ = 60^\circ $
\(\widehat {ACD}\) là góc nội tiếp chắn cung \(AD\) nên \(\widehat {ACD} = \dfrac{{60^\circ }}{2} = 30^\circ \) .
Hướng dẫn giải:
Sử dụng:
+ Góc nội tiếp có số đo bằng nửa số đo cung bị chắn
+ Góc có đỉnh bên trong đường tròn có số đo bằng nửa tổng số đo hai cung bị chắn
