Trả lời bởi giáo viên
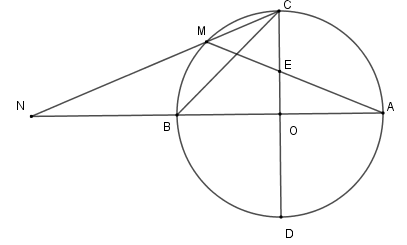
Xét \(\left( O \right)\) có \(\widehat {CNA}\) là góc có đỉnh bên ngoài đường tròn nên \(\widehat {CNB} = \dfrac{1}{2}\) (số đo cung \(AC - \) số đo cung \(MB\) )
Mà số đo cung \(MB = \dfrac{1}{2}\) số đo cung \(AC\) nên \(\widehat {CNA} = \dfrac{1}{2}\)số đo cung \(MB\) .
Lại có \(\widehat {MCB} = \dfrac{1}{2}\) số đo cung \(MB\) (góc nội tiếp) nên \(\widehat {MCB} = \widehat {BNC} \Rightarrow \Delta BNC\) cân tại \(B \Rightarrow BN = BC\)
Xét \(\Delta COB\) vuông cân tại \(O\) ta có \(BC = \sqrt {O{C^2} + O{B^2}} = R\sqrt 2 \) nên \(BN = R\sqrt 2 \)
Suy ra \(NO = NB + OB = R + \sqrt 2 R = R\left( {1 + \sqrt 2 } \right)\)
Khi đó \({S_{ONC}} = \dfrac{1}{2}NO.CO = \dfrac{1}{2}.\left( {1 + \sqrt 2 } \right)R.R = \dfrac{{\sqrt 2 + 1}}{2}{R^2}\) .
Hướng dẫn giải:
Sử dụng định lý Pytago và công thức diện tích tam giác \(S = \dfrac{1}{2}ah\) với \(h\) là chiều cao ứng với cạnh đáy là \(a.\)

