Câu hỏi:
2 năm trước
Cho \(\left( {O;R} \right)\) và dây \(AB\) bất kỳ. Gọi \(M\) là điểm chính giữa cung nhỏ \(AB\) , \(E;F\) là hai điểm bất kỳ trên dây \(AB\) . Gọi \(C,D\) lần lượt là giao điểm của \(ME;MF\) với \(\left( O \right)\) . Khi đó \(\widehat {CEF} + \widehat {CDF}\) bằng
Trả lời bởi giáo viên
Đáp án đúng: d
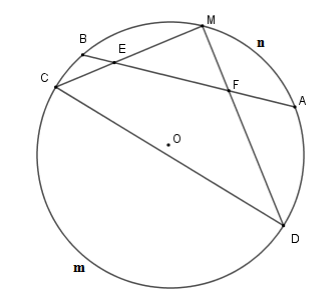
Ta có \(\widehat {CEF}\) là góc có đỉnh bên trong đường tròn nên \(\widehat {CEF} = \dfrac{1}{2}\)(sđ \(\overparen{AmC} + \) sđ \(\overparen{BM}\) )
Và \(\widehat {MDC} = \dfrac{1}{2}\) sđ\(\overparen{MC}\) (góc nội tiếp chắn cung \(MC\))
Từ đó \(\widehat {CEF} + \widehat {CDF} = \dfrac{1}{2}\) (sđ\(\overparen{AmC} + \) sđ \(\overparen{BM}\)$ + $ sđ \(\overparen{MC})\)
Mà cung $AnM = $ cung \(MB\) nên \(\widehat {EFD} + \widehat {ECD} \)
\(= \dfrac{1}{2}\) (sđ\(\overparen{AmC} + \) sđ \(\overparen{AnM}\)$ + $ sđ \(\overparen{MC}\)) =$\dfrac{1}{2}.360^\circ = 180^\circ .$
Hướng dẫn giải:
Sử dụng:
+ Góc nội tiếp có số đo bằng nửa số đo cung bị chắn
+ Góc có đỉnh bên trong đường tròn có số đo bằng nửa tổng số đo hai cung bị chắn
