Chọn khẳng định đúng. Cho đường tròn $\left( O \right)$ có cung $MN < $ cung \(PQ\), khi đó
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
+) Cung lớn hơn căng dây lớn hơn.
+) Dây lớn hơn căng cung lớn hơn.
Nên cung $MN < $ cung \(PQ\) thì \(MN < PQ.\)
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là sai?
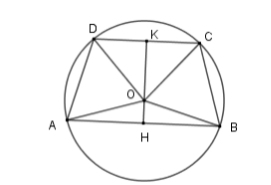
Kẻ $KH \bot CD$ và $AB$ lần lượt tại $K$ và $H$.
Suy ra $OK$ vừa là đường cao, vừa là đường phân giác của $\widehat {DOC}$$ \Rightarrow \widehat {DOK} = \widehat {COK}$
Và $OH$ vừa là đường cao, vừa là đường phân giác của $\widehat {AOB}$$ \Rightarrow \widehat {AOH} = \widehat {BOH}$
Do đó $\widehat {AOH} + \widehat {DOK} = \widehat {BOH} + \widehat {COK} \Rightarrow \widehat {AOD} = \widehat {COB}$
Nên số đo cung $AD$ bằng số đo cung $BC$, từ đó $AD = BC$.
Vì \(DC//AB;AD = BC\) nên \(ABCD\) là hình thang cân nên \(AC = BD\)
Phương án A, B, D đúng và C sai.
Cho đường tròn (O) đường kính $AB$ và một cung $AC$ có số đo bằng $50^\circ $. Vẽ dây $CD$ vuông góc với $AB$ và dây $DE$ song song với $AB$. Chọn kết luận sai?
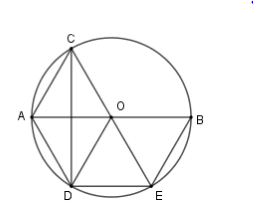
Vì cung \(AC\) có số đo \(50^\circ \) nên \(\widehat {AOC} = 50^\circ \)
Vì $AO \bot CD;AO{\rm{//}}DE \Rightarrow CD \bot DE$$ \Rightarrow \widehat {CDE} = 90^\circ $ mà $C,D,E \in \left( O \right)$ nên $CE$ là đường kính hay $C;O;E$ thẳng hàng
Xét $\left( O \right)$ có $OA$ là đường cao trong tam giác cân $ODC$ nên $OA$ cũng là đường phân giác $ \Rightarrow \widehat {COA} = \widehat {AOD} = 50^\circ $
Lại thấy $\widehat {BOE} = \widehat {AOC} = 50^\circ $ (đối đỉnh) suy ra $\widehat {AOC} = \widehat {AOD} = \widehat {BOE} = 50^\circ $ (D đúng) và suy ra cung $AC$ bằng cung $BE$ nên B đúng.
Ta có \(\widehat {DOE} = 180^\circ - \widehat {AOD} - \widehat {BOE} = 80^\circ \) nên cung \(AD < \) cung \(DE \Rightarrow AD < DE\) hay đáp án A sai.
Lại có \(\widehat {AOE} = \widehat {AOD} + \widehat {DOE} = 50^\circ + 80^\circ = 130^\circ \) và \(\widehat {BOD} = \widehat {BOE} + \widehat {DOE} = 50^\circ + 80^\circ = 130^\circ \)
Nên \(\widehat {AOE} = \widehat {BOD}\) suy ra số đo cung \(AE = \) số đo cung \(BD.\) Do đó C đúng.
Phương án B, C, D đúng và A sai.
Chọn khẳng định sai.
+) Trong một đường tròn, đường kính đi qua trung điểm của một dây ( không đi qua tâm ) thì đi qua điểm chính giữa của cung bị căng bởi dây ấy.
+) Trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.
+) Trong một đường tròn, cung lớn hơn căng dây lớn hơn.
+) Hai đường kính của đường tròn luôn bằng nhau nhưng chưa chắc đã vuông góc với nhau.
Suy ra A, B, C đúng, D sai.
Cho tam giác $ABC$ cân tại $A$ và $\widehat A = 70^\circ $ nội tiếp đường tròn $\left( O \right)$. Trong các cung nhỏ $AB;BC;AC$, cung nào là cung nhỏ nhất?
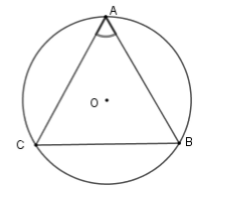
Vì tam giác $ABC$ cân tại $A$ có $\widehat A = 70^\circ \Rightarrow \widehat B = \widehat C = \dfrac{{180^\circ - \widehat A}}{2} = \dfrac{{180^\circ - 70^\circ }}{2} = 55^\circ $
Vì $\widehat A > \widehat B = \widehat C$ nên theo mối liên hệ giữa cạnh và góc trong tam giác ta có $BC > AB = AC$
Theo mối liên hệ giữa cung và dây ta có cung $BC$ $ > $ cung $AB$ $ = $ cung $AC$.
Cho đường tròn $\left( {O;R} \right)$ và hai dây $MN;EF$ sao cho $\widehat {MON} = 120^\circ ;\widehat {EOF} = 90^\circ $. Chọn đáp án đúng.
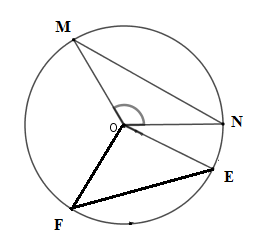
Vì $\widehat {EOF} < \widehat {MON}$ nên cung $EF$ nhỏ hơn cung $MN$, từ đó dây $EF < MN$ (*)
Xét tam giác $OEF$ cân tại $O$ có $\widehat {EOF} = 90^\circ $ nên theo định lý Pytago ta có $E{F^2} = O{F^2} + O{E^2} = {R^2} + {R^2} = 2{R^2}$
\( \Rightarrow EF = \sqrt 2 R.\) (**)
$MN$ là dây không đi qua tâm nên $MN < 2R$ (***)
Từ (*) , (**) và (***) ta có $\sqrt 2 R < MN < 2R$
Cho tam giác $ABC$ có $\widehat B = 30^\circ $, đường trung tuyến $AM$, đường cao $CH$. Vẽ đường tròn ngoại tiếp $BHM$. Kết luận nào sai khi nói về các cung $HB;MB;MH$ của đường tròn ngoại tiếp tam giác $MHB$ ?
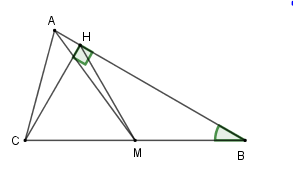
Vì trong một đường tròn hai cung bằng nhau căng hai dây bằng nhau nên ta đi so sánh các đoạn thẳng $HB;MB;MH$.
Xét tam giác $BCH$ vuông tại $H$ có $\cos B = \dfrac{{HB}}{{BC}} \Leftrightarrow \dfrac{{HB}}{{BC}} = \cos 30^\circ = \dfrac{{\sqrt 3 }}{2} \Rightarrow HB = \dfrac{{\sqrt 3 }}{2}BC$ (*)
Xét tam giác \(HBC\) vuông tại \(H\) có \(HM\) là trung tuyến ứng với cạnh huyền nên \(HM = BM = CM = \dfrac{{BC}}{2}\) (**)
Mà \(\dfrac{{BC}}{2} < \dfrac{{\sqrt 3 }}{2}BC\) nên từ (*) và (**) ta có \(BM = HM < HB\)
Suy ra cung $MB = $ cung \(HM < \) cung \(HB\).
Hay cung \(HB\) là cung lớn nhất nên B sai.
Cho đường tròn $\left( {O;R} \right)$, dây cung $AB = R\sqrt 2 $. Vẽ đường kính $CD \bot AB$ ($C$ thuộc cung lớn $AB$). Trên cung $AC$ nhỏ lấy điểm $M$, vẽ dây $AN{\rm{//}}CM$. Độ dài đoạn $MN$ là
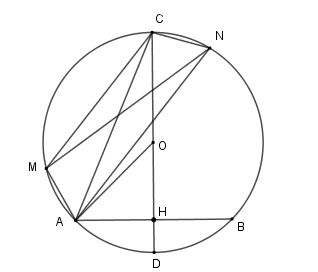
Vì hai dây $MC{\rm{//}}AN$ nên hai cung $AM$ và cung $CN$ bằng nhau, hay $AM = CN$
Suy ra $MCNA$ là hình thang cân $ \Rightarrow MN = AC$.
Gọi $H$ là giao của $CD$ và $AB$. Khi đó vì $AB \bot CD$ tại $H$ nên $H$ là trung điểm của $AB \Rightarrow AH = \dfrac{{AB}}{2} = \dfrac{{R\sqrt 2 }}{2}$
Xét tam giác vuông $AHO$, theo định lý Pytago ta có $OH = \sqrt {A{O^2} - A{H^2}} = \sqrt {{R^2} - {{\left( {\dfrac{{R\sqrt 2 }}{2}} \right)}^2}} = \dfrac{{R\sqrt 2 }}{2}$
$ \Rightarrow CH = R + \dfrac{{R\sqrt 2 }}{2} = \dfrac{{2 + \sqrt 2 }}{2}R$
Theo định lý Pytago cho tam giác $ACH$ vuông ta có $AC = \sqrt {C{H^2} + A{H^2}} = \sqrt {\dfrac{{{{\left( {2 + \sqrt 2 } \right)}^2}}}{4}{R^2} + \dfrac{{2{R^2}}}{4}} = \sqrt {\dfrac{{8 + 4\sqrt 2 }}{4}{R^2}} = \sqrt {2 + \sqrt 2 } .R$
Vậy $MN = R\sqrt {2 + \sqrt 2 } $.
Cho đường tròn $(O;R)$ có hai dây cung $AB$ và $CD$ vuông góc với nhau tại $I$ ( $C$ thuộc cung nhỏ $AB$ ). Kẻ đường kính $BE$ của $(O)$. Đẳng thức nào sau đây là sai?
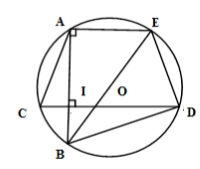
Xét $\left( O \right)$ có $BE$ là đường kính và $A \in \left( O \right)$$ \Rightarrow AE \bot AB$ mà $CD \bot AB$$ \Rightarrow AE{\rm{//}}CD$
Nên cung $AC$ bằng cung $ED$ hay $AC = ED$
Xét các tam giác vuông $\Delta IAC$ và $\Delta IBD$ ta có $I{A^2} + I{C^2} = A{C^2};I{B^2} + I{D^2} = B{D^2} $$\Rightarrow I{A^2} + I{C^2} + I{B^2} + I{D^2} = A{C^2} + B{D^2} $$= E{D^2} + B{D^2}$
Mà $\Delta BED$ vuông tại $D$ nên $E{D^2} + B{D^2} = E{B^2}$
Hay $I{A^2} + I{C^2} + I{B^2} + I{D^2} = B{E^2}$ nên C đúng mà \(BE \ne AD\) nên D sai.
Xét các tam giác vuông $\Delta IAD$ và $\Delta IBC$ ta có
$I{A^2} + I{D^2} = A{D^2};I{B^2} + I{C^2} = B{C^2}$$ \Rightarrow I{A^2} + I{C^2} + I{B^2} + I{D^2} = A{D^2} + B{C^2}$
Vậy A, B, C đúng, D sai.
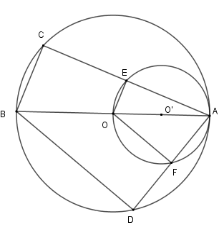
So sánh dây $AE$ và $AF$ của đường tròn $(O')$.
_ban_kinh_R.PNG)
Vì \(OA\) là đường kính của đường tròn \(\left( {O'} \right)\) và \(E,F \in \left( {O'} \right)\) nên \(\Delta OEA\) vuông tại \(E;\,\Delta OFA\) vuông tại \(F.\)
Theo định lý Pytago cho tam giác vuông \(OEA\) và \(OFA\) ta có : $A{E^2} = A{O^2} - O{E^2}$ và $A{F^2} = A{O^2} - A{E^2}$ mà $OE = OF$ (theo câu trước)
$ \Rightarrow A{E^2} = A{F^2} \Rightarrow AE = AF$.
So sánh cung $OE$ và cung $OF$ của đường tròn $(O')$.
_ban_kinh_R.PNG)
Xét $\left( {O'} \right)$ có $OA$ là đường kính và $E \in \left( {O'} \right)$ nên $OE \bot AC$
Tương tự với $\left( O \right)$ ta có $BC \bot AC$ nên $OE{\rm{//}}BC$ mà $O$ là trung điểm của $AB$
$ \Rightarrow $ $E$ là trung điểm của $AC$ $ \Rightarrow $ $OE = \dfrac{1}{2}BC.$
Tương tự $OF = \dfrac{1}{2}DB$ mà cung $BC$ bằng cung $BD$ nên $BC = BD \Rightarrow OE = OF$ hay cung \(OE = \) cung \(OF.\)
So sánh cung $OE$ và cung $OF$ của đường tròn $(O')$.
_ban_kinh_R.PNG)
Xét $\left( {O'} \right)$ có $OA$ là đường kính và $E \in \left( {O'} \right)$ nên $OE \bot AC$
Tương tự với $\left( O \right)$ ta có $BC \bot AC$ nên $OE{\rm{//}}BC$ mà $O$ là trung điểm của $AB$
$ \Rightarrow $ $E$ là trung điểm của $AC$ $ \Rightarrow $ $OE = \dfrac{1}{2}BC.$
Tương tự $OF = \dfrac{1}{2}DB$ mà cung $BC$ bằng cung $BD$ nên $BC = BD \Rightarrow OE = OF$ hay cung \(OE = \) cung \(OF.\)
So sánh dây $OE$ và $OF$ của đường tròn $(O')$.
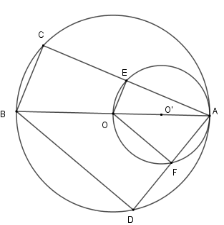
Xét $\left( {O'} \right)$ có $OA$ là đường kính và $E \in \left( {O'} \right)$ nên $OE \bot AC$
Tương tự với $\left( O \right)$ ta có $BC \bot AC$ nên $OE{\rm{//}}BC$ mà $O$ là trung điểm của $AB$
$ \Rightarrow $ $E$ là trung điểm của $AC$
$ \Rightarrow $ $OE = \dfrac{1}{2}BC.$
Tương tự $OF = \dfrac{1}{2}DB$ mà cung $BC$ nhỏ hơn cung $BD$ nên
$BC < BD \Rightarrow OE < OF$ .
So sánh dây $AE$ và $AF$ của đường tròn $(O')$.
Theo định lý Pytago ta có : $A{E^2} = A{O^2} - O{E^2}$ và $A{F^2} = A{O^2} - O{F^2}$ mà $OE < OF$
$ \Rightarrow A{E^2} > A{F^2} \Rightarrow AE > AF$.
So sánh dây $OE$ và $OF$ của đường tròn $(O')$.

Xét $\left( {O'} \right)$ có $OA$ là đường kính và $E \in \left( {O'} \right)$ nên $OE \bot AC$
Tương tự với $\left( O \right)$ ta có $BC \bot AC$ nên $OE{\rm{//}}BC$ mà $O$ là trung điểm của $AB$
$ \Rightarrow $ $E$ là trung điểm của $AC$
$ \Rightarrow $ $OE = \dfrac{1}{2}BC.$
Tương tự $OF = \dfrac{1}{2}DB$ mà cung $BC$ nhỏ hơn cung $BD$ nên
$BC < BD \Rightarrow OE < OF$ .
So sánh dây $OE$ và $OF$ của đường tròn $(O')$.

Xét $\left( {O'} \right)$ có $OA$ là đường kính và $E \in \left( {O'} \right)$ nên $OE \bot AC$
Tương tự với $\left( O \right)$ ta có $BC \bot AC$ nên $OE{\rm{//}}BC$ mà $O$ là trung điểm của $AB$
$ \Rightarrow $ $E$ là trung điểm của $AC$
$ \Rightarrow $ $OE = \dfrac{1}{2}BC.$
Tương tự $OF = \dfrac{1}{2}DB$ mà cung $BC$ nhỏ hơn cung $BD$ nên
$BC < BD \Rightarrow OE < OF$ .
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là đúng?
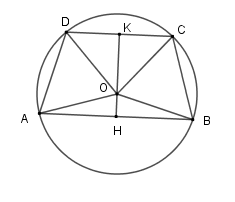
Kẻ $KH \bot CD$ và $KH \bot AB$ lần lượt tại $K$ và $H$.
Suy ra $OK$ vừa là đường cao, vừa là đường phân giác của $\widehat {DOC}$ $ \Rightarrow \widehat {DOK} = \widehat {COK}$
Và $OH$ vừa là đường cao, vừa là đường phân giác của $\widehat {AOB}$ $ \Rightarrow \widehat {AOH} = \widehat {BOH}$
Do đó $\widehat {AOH} + \widehat {DOK} = \widehat {BOH} + \widehat {COK} \Rightarrow \widehat {AOD} = \widehat {COB}$
Nên số đo cung $AD$ bằng số đo cung $BC$, từ đó $AD = BC$.
Phương án A, C, D sai, B đúng.
Chọn khẳng định đúng. Cho đường tròn $\left( O \right)$ có dây $AB > CD$ khi đó
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
+) Cung lớn hơn căng dây lớn hơn.
+) Dây lớn hơn căng cung lớn hơn.
Nên dây $AB > CD$ thì cung $AB$ lớn hơn cung $CD$
Cho đường tròn $\left( O \right)$ có hai dây $AB,CD$ song song với nhau. Kết luận nào sau đây là đúng?
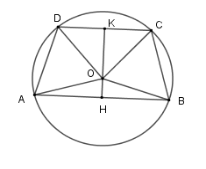
Kẻ $KH \bot CD$ và $KH \bot AB$ lần lượt tại $K$ và $H$.
Suy ra $OK$ vừa là đường cao, vừa là đường phân giác của $\widehat {DOC}$$ \Rightarrow \widehat {DOK} = \widehat {COK}$
Và $OH$ vừa là đường cao, vừa là đường phân giác của $\widehat {AOB}$$ \Rightarrow \widehat {AOH} = \widehat {BOH}$
Do đó $\widehat {AOH} + \widehat {DOK} = \widehat {BOH} + \widehat {COK} \Rightarrow \widehat {AOD} = \widehat {COB}$
Nên số đo cung $AD$ bằng số đo cung $BC$, từ đó $AD = BC$.
Phương án A, C, D sai và B đúng.
Cho đường tròn $(O)$ đường kính $AB$ và một cung $AC$ có số đo nhỏ hơn $90^\circ $. Vẽ dây $CD$ vuông góc với $AB$ và dây $DE$ song song với $AB$. Chọn kết luận sai?
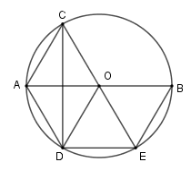
Vì $AO \bot CD;AO{\rm{//}}DE \Rightarrow CD \bot DE$$ \Rightarrow \widehat {CDE} = 90^\circ $ mà $C,D,E \in \left( O \right)$ nên $CE$ là đường kính hay $C;O;E$ thẳng hàng
Xét $\left( O \right)$ có $OA$ là đường cao trong tam giác cân $ODC$ nên $OA$ cũng là đường phân giác $ \Rightarrow \widehat {COA} = \widehat {AOD}$
Suy ra cung $AD$ bằng cung $AC$ nên dây $AD = AC$
Lại thấy $\widehat {AOC} = \widehat {BOE}$ (đối đỉnh) nên cung $AC$ bằng cung $BE$ suy ra dây $AC = BE$.
Phương án A, B, C đúng.

