Câu hỏi:
2 năm trước
Cho đường tròn $(O;R)$ có hai dây cung $AB$ và $CD$ vuông góc với nhau tại $I$ ( $C$ thuộc cung nhỏ $AB$ ). Kẻ đường kính $BE$ của $(O)$. Đẳng thức nào sau đây là sai?
Trả lời bởi giáo viên
Đáp án đúng: d
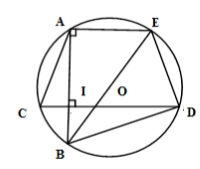
Xét $\left( O \right)$ có $BE$ là đường kính và $A \in \left( O \right)$$ \Rightarrow AE \bot AB$ mà $CD \bot AB$$ \Rightarrow AE{\rm{//}}CD$
Nên cung $AC$ bằng cung $ED$ hay $AC = ED$
Xét các tam giác vuông $\Delta IAC$ và $\Delta IBD$ ta có $I{A^2} + I{C^2} = A{C^2};I{B^2} + I{D^2} = B{D^2} $$\Rightarrow I{A^2} + I{C^2} + I{B^2} + I{D^2} = A{C^2} + B{D^2} $$= E{D^2} + B{D^2}$
Mà $\Delta BED$ vuông tại $D$ nên $E{D^2} + B{D^2} = E{B^2}$
Hay $I{A^2} + I{C^2} + I{B^2} + I{D^2} = B{E^2}$ nên C đúng mà \(BE \ne AD\) nên D sai.
Xét các tam giác vuông $\Delta IAD$ và $\Delta IBC$ ta có
$I{A^2} + I{D^2} = A{D^2};I{B^2} + I{C^2} = B{C^2}$$ \Rightarrow I{A^2} + I{C^2} + I{B^2} + I{D^2} = A{D^2} + B{C^2}$
Vậy A, B, C đúng, D sai.
Hướng dẫn giải:
Bước 1: Sử dụng tính chất hai cung bị chắn giữa hai dây song song thì bằng nhau để chứng minh $AC = ED$
Bước 2: Sử dụng định lý Pytago để chứng minh hệ thức.
