Câu hỏi:
2 năm trước
Cho tam giác $ABC$ có $\widehat B = 30^\circ $, đường trung tuyến $AM$, đường cao $CH$. Vẽ đường tròn ngoại tiếp $BHM$. Kết luận nào sai khi nói về các cung $HB;MB;MH$ của đường tròn ngoại tiếp tam giác $MHB$ ?
Trả lời bởi giáo viên
Đáp án đúng: b
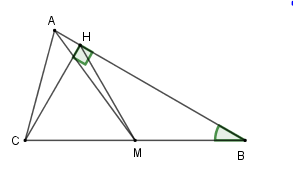
Vì trong một đường tròn hai cung bằng nhau căng hai dây bằng nhau nên ta đi so sánh các đoạn thẳng $HB;MB;MH$.
Xét tam giác $BCH$ vuông tại $H$ có $\cos B = \dfrac{{HB}}{{BC}} \Leftrightarrow \dfrac{{HB}}{{BC}} = \cos 30^\circ = \dfrac{{\sqrt 3 }}{2} \Rightarrow HB = \dfrac{{\sqrt 3 }}{2}BC$ (*)
Xét tam giác \(HBC\) vuông tại \(H\) có \(HM\) là trung tuyến ứng với cạnh huyền nên \(HM = BM = CM = \dfrac{{BC}}{2}\) (**)
Mà \(\dfrac{{BC}}{2} < \dfrac{{\sqrt 3 }}{2}BC\) nên từ (*) và (**) ta có \(BM = HM < HB\)
Suy ra cung $MB = $ cung \(HM < \) cung \(HB\).
Hay cung \(HB\) là cung lớn nhất nên B sai.
Hướng dẫn giải:
Sử dụng mối liên hệ giữa cung và dây
Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
Hai cung bằng nhau căng hai dây bằng nhau và ngược lại
