Giả sử \(OA = a;MC = 2a\) . Độ dài \(CH\) là
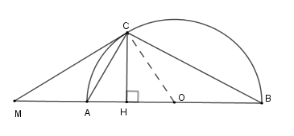
Theo định lý Pytago cho tam giác \(MCO\) vuông ta có \(MO = \sqrt {O{C^2} + M{C^2}} = a\sqrt 5 \)
Xét tam giác \(MCO\) vuông ta có \(MC.CO = CH.MO \Rightarrow CH = \dfrac{{2{a^2}}}{{\sqrt 5 a}} = \dfrac{{2\sqrt 5 a}}{5}\) .
\(CA\) là tia phân giác của góc nào dưới đây
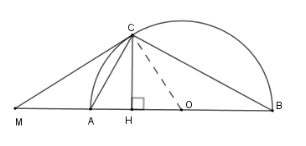
Xét nửa $\left( O \right)$ có \(\widehat {MCA} = \widehat {CBA}\) (*) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AC\) )
Lại có \(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Xét tam giác \(ACH\) vuông tại \(H\) có \(\widehat {ACH}+ \widehat {CAH}=90^0\) (1)
Xét tam giác \(ACB\) vuông tại \(C\) có \(\widehat {CBA}+ \widehat {CAH}=90^0\) (2)
Từ (1) và (2) suy ra \(\widehat {ACH} = \widehat {CBA}\) (**) (cùng phụ với góc \(\widehat {CAB}\) )
Từ (*) và (**) ta có \(\widehat {MCA} = \widehat {ACH}\) nên \(CA\) là tia phân giác của góc \(\widehat {MCH}\) .
\(CA\) là tia phân giác của góc nào dưới đây

Xét nửa $\left( O \right)$ có \(\widehat {MCA} = \widehat {CBA}\) (*) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AC\) )
Lại có \(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Xét tam giác \(ACH\) vuông tại \(H\) có \(\widehat {ACH}+ \widehat {CAH}=90^0\) (1)
Xét tam giác \(ACB\) vuông tại \(C\) có \(\widehat {CBA}+ \widehat {CAH}=90^0\) (2)
Từ (1) và (2) suy ra \(\widehat {ACH} = \widehat {CBA}\) (**) (cùng phụ với góc \(\widehat {CAB}\) )
Từ (*) và (**) ta có \(\widehat {MCA} = \widehat {ACH}\) nên \(CA\) là tia phân giác của góc \(\widehat {MCH}\) .
Hệ thức nào dưới đây là đúng.
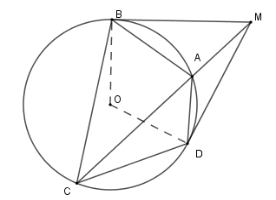
Tương tự câu trước ta có \(\Delta MAD\backsim \Delta MDC\left( {g - g} \right) \)\(\Rightarrow \dfrac{{MD}}{{MC}} = \dfrac{{AD}}{{DC}}\)
Mà theo câu trước ta có \(\dfrac{{MB}}{{MC}} = \dfrac{{BA}}{{CB}}\)
Theo tính chất hai tiếp tuyến cắt nhau thì \(MB = MD\) nên \(\dfrac{{AD}}{{DC}} = \dfrac{{AB}}{{BC}} \Leftrightarrow AD.BC = AB.DC\)
Khi đó \(MA.MC\) bằng
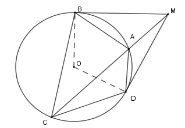
Xét \(\left( O \right)\) có \(\widehat {MBA} = \widehat {BCA}\) (góc tạo bởi tiếp tuyến và dây cung \(AB\) bằng góc nội tiếp chắn cung \(AB\) )
Suy ra \(\Delta MBA\backsim\Delta MCB\left( {g - g} \right) \)
\(\Rightarrow \dfrac{{MB}}{{MC}} = \dfrac{{MA}}{{MB}} = \dfrac{{BA}}{{CB}} \)
\(\Rightarrow MA.MC = M{B^2}\)
Khi đó \(MA.MC\) bằng

Xét \(\left( O \right)\) có \(\widehat {MBA} = \widehat {BCA}\) (góc tạo bởi tiếp tuyến và dây cung \(AB\) bằng góc nội tiếp chắn cung \(AB\) )
Suy ra \(\Delta MBA\backsim\Delta MCB\left( {g - g} \right) \)
\(\Rightarrow \dfrac{{MB}}{{MC}} = \dfrac{{MA}}{{MB}} = \dfrac{{BA}}{{CB}} \)
\(\Rightarrow MA.MC = M{B^2}\)
Tia phân giác trong góc $A$ cắt $BC$ và \((O)\) lần lượt tại $D$ và $M$. Khi đó \(MA.MD\) bằng
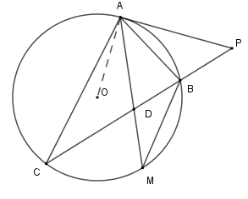
Xét đường tròn \((O)\) có \(\widehat {MBC} = \widehat {MAC}\) (hai góc nội tiếp cùng chắn cung MC)
Lại có \(\widehat {MAB} = \widehat {MAC}\) (do AM là phân giác góc BAC)
Suy ra \(\widehat {MBD} = \widehat {MAB}\) (cùng bằng \(\widehat {MAC}\) )
Xét \(\Delta MBD\) và \(\Delta MAB\) có \(\widehat M\) chung và \(\widehat {MBD} = \widehat {MAB}\) (chứng minh trên)
Nên \(\Delta MBD\backsim\Delta MAB\left( {g - g} \right) \)\(\Rightarrow \dfrac{{MB}}{{MA}} = \dfrac{{MD}}{{MB}} \)\(\Rightarrow MA.MD = M{B^2}\)
Hai tam giác nào sau đây đồng dạng?
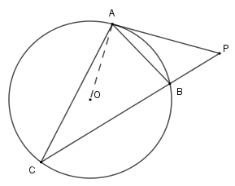
Xét \(\left( O \right)\) có \(\widehat {ACB} = \widehat {BAP}\) (hệ quả) suy ra \(\Delta PAC\backsim\Delta PBA\left( {g - g} \right)\) .
Hai tam giác nào sau đây đồng dạng?

Xét \(\left( O \right)\) có \(\widehat {ACB} = \widehat {BAP}\) (hệ quả) suy ra \(\Delta PAC\backsim\Delta PBA\left( {g - g} \right)\) .
Giả sử $MK$cắt $(O)$ tại $C$. Đường thẳng \(MA\) song song với đường thẳng
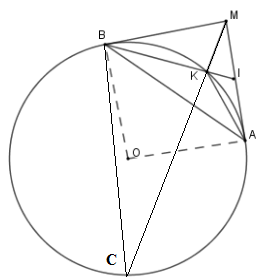
Vì \(\Delta IKM\backsim\Delta IMB\left( {c - g - c} \right)\) \( \Rightarrow \widehat {IMK} = \widehat {MBI}\) mà \(\widehat {MBI} = \widehat {MCB}\) (hệ quả)
Nên \(\widehat {BCM} = \widehat {CMA}\) mà hai góc ở vị trí so le trong nên \(MA{\rm{//}}BC\) .
Tam giác nào dưới đây đồng dạng với tam giác \(IKM\)?
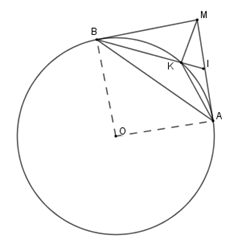
\(\Delta IKA\backsim\Delta IAB\left( {g - g} \right)\) (câu trước) \( \Rightarrow \dfrac{{IK}}{{IA}} = \dfrac{{IA}}{{IB}}\) mà \(IA = IM \Rightarrow \dfrac{{IK}}{{IM}} = \dfrac{{IM}}{{IB}}\) nên \(\Delta IKM\backsim\Delta IMB\left( {c - g - c} \right)\)
Tam giác \(IKA\) đồng dạng với tam giác
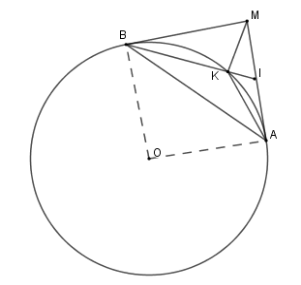
Ta có \(\widehat {IAK} = \widehat {IBA}\) (hệ quả) nên \(\Delta IKA\backsim\Delta IAB\left( {g - g} \right)\)
Tam giác \(IKA\) đồng dạng với tam giác

Ta có \(\widehat {IAK} = \widehat {IBA}\) (hệ quả) nên \(\Delta IKA\backsim\Delta IAB\left( {g - g} \right)\)
Hệ thức nào dưới đây đúng .
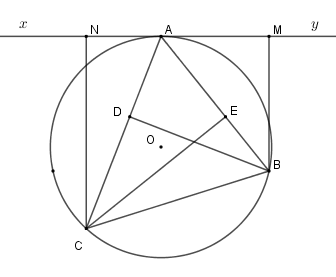
Từ câu trước, ta có \(\dfrac{{AM}}{{CD}} = \dfrac{{AB}}{{CB}}\)
Tương tự ta có \(\Delta ANC\backsim\Delta BEC\left( {g - g} \right) \)
\(\Rightarrow \dfrac{{BE}}{{AN}} = \dfrac{{BC}}{{AC}}\)
Suy ra \(\dfrac{{AM}}{{CD}}.\dfrac{{BE}}{{AN}} = \dfrac{{AB}}{{BC}}.\dfrac{{BC}}{{AC}}\)
\(\Leftrightarrow \dfrac{{AB}}{{AC}} = \dfrac{{MA.BE}}{{NA.CD}}\)
Tam giác \(AMB\) đồng dạng với tam giác
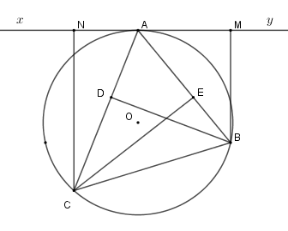
Xét \(\left( O \right)\) có \(\widehat {MAB} = \widehat {ACB}\) (hệ quả) \( \Rightarrow \Delta AMB\backsim\Delta CDB\left( {g - g} \right)\)
Tam giác \(AMB\) đồng dạng với tam giác

Xét \(\left( O \right)\) có \(\widehat {MAB} = \widehat {ACB}\) (hệ quả) \( \Rightarrow \Delta AMB\backsim\Delta CDB\left( {g - g} \right)\)
Trong hình vẽ dưới đây, biết \(CF\) là tiếp tuyến của đường tròn \(\left( O \right)\).Hãy chỉ ra góc tạo bởi tiếp tuyến và dây cung?
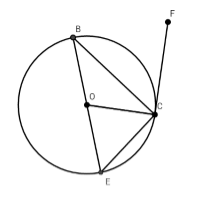
Đường tròn tâm \((O)\) có \(CF\) là tia tiếp tuyến tại tiếp điểm $A$ và dây cung $BC.$ Nên góc \(BCF\) là góc tạo bởi tia tiếp tuyến và dây cung.
\(CA\) là tia phân giác của góc nào dưới đây

Xét nửa $\left( O \right)$ có \(\widehat {MCA} = \widehat {CBA}\) (*) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AC\) )
Lại có \(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Xét tam giác \(ACH\) vuông tại \(H\) có \(\widehat {ACH}+ \widehat {CAH}=90^0\) (1)
Xét tam giác \(ACB\) vuông tại \(C\) có \(\widehat {CBA}+ \widehat {CAH}=90^0\) (2)
Từ (1) và (2) suy ra \(\widehat {ACH} = \widehat {CBA}\) (**) (cùng phụ với góc \(\widehat {CAB}\) )
Từ (*) và (**) ta có \(\widehat {MCA} = \widehat {ACH}\) nên \(CA\) là tia phân giác của góc \(\widehat {MCH}\) .
Tìm số đo góc \(\widehat {xAB}\). trong hình vẽ biết \(\widehat {AOB} = {100^0}\) và \(Ax\) là tiếp tuyến của đường tròn \((O)\) tại \(A.\)
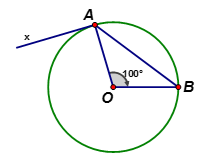
Xét đường tròn \(\left( O \right)\) có \(\widehat {AOB} = 100^\circ \) nên số đo cung \(AB\) nhỏ bằng \(100^\circ \)
Suy ra số đo cung \(AB\) lớn bằng \(360^\circ - 100^\circ = 260^\circ \)
Lại có \(\widehat {xAB}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung \(AB\) lớn nên \(\widehat {xAB} = \dfrac{1}{2}.260^\circ = 130^\circ \) .
Khi đó \(MA.MC\) bằng

Xét \(\left( O \right)\) có \(\widehat {MBA} = \widehat {BCA}\) (góc tạo bởi tiếp tuyến và dây cung \(AB\) bằng góc nội tiếp chắn cung \(AB\) )
Suy ra \(\Delta MBA\backsim\Delta MCB\left( {g - g} \right) \)
\(\Rightarrow \dfrac{{MB}}{{MC}} = \dfrac{{MA}}{{MB}} = \dfrac{{BA}}{{CB}} \)
\(\Rightarrow MA.MC = M{B^2}\)

