Diện tích hình tròn bán kính R=8cm là
Diện tích S=πR2=π.82=64π(cm2).
Một hình tròn có diện tích S=225π(cm2) . Bán kính của hình tròn đó là:
Diện tích S=πR2=225π⇔R2=225⇒R=15(cm).
Cho đường tròn (O,8cm), đường kính AB. Điểm M∈(O) sao cho ^BAM=600. Tính diện tích hình quạt AOM .
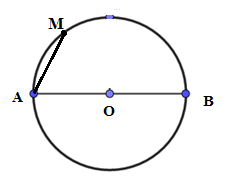
Xét đường tròn (O) có^BAM=60∘ suy ra số đo cung MB bằng 2.60∘=120∘
Suy ra số đo cung AM bằng n∘=180∘−120∘=60∘
Vậy diện tích hình quạt AOM là S=πR2n360=π.82.60360=32π3(cm2)
Cho đường tròn (O) đường kính AB= 3√3cm . Điểm C∈(O) sao cho ^ABC=600. Tính diện tích hình viên phânBC . (Hình viên phân là phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy)
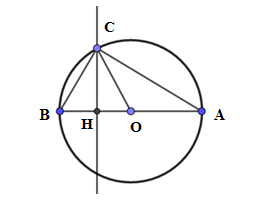
Xét đường tròn (O) có:
^ACB=90∘ (góc nội tiếp chắn nửa đường tròn)
Suy ra ^CAB=90∘−^CBA=30∘ (tam giác ABC vuông tại C)
^ACB và ^BOC là góc nội tiếp và góc ở tâm cùng chắn cung AC ⇒^BOC=2.^ACB=2.300=600⇒SquạtAOC=πR2.60360=πR26
Xét ΔBOC có ^BOC=60∘ và OA=OC=R nên tam giác AOC đều cạnh bằng R .
Gọi CH là đường cao của tam giác AOC , ta có:
CH=CO.sin600=√32.R⇒SAOC=12CH.OA=12.√32.R.R=√34.R2.
Diện tích hình viên phân BC là:
SquạtBOC−SΔBOC=πR26−√34.R2=(π6−√34).R2=(2π−3√312).(3√32)2=18π−27√316(cm2).
Cho hình vuông có cạnh là 6cm nội tiếp đường tròn (O). Hãy tính diện tích hình tròn (O).
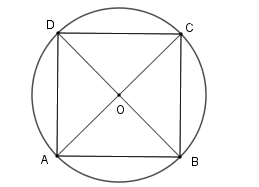
Gọi hình vuông ABCD nội tiếp đường tròn (O) khi đó OA=OB=OC=OD=R⇒O là giao điểm của AC và BD ⇒R=AC2 .
Xét tam giác vuông ABC ta có AC2=AB2+BC2=62+62=72⇒AC=6√2⇒R=6√22=3√2
Diện tích hình tròn (O) là S=πR2=π(3√2)2=18π(cm2)
Cho đường tròn (O) đường kính AB=4√2cm. Điểm C∈(O) sao cho ^ABC=300. Tính diện tích hai hình viên phân giới hạn bởi nửa đường tròn (O) và dây AC,BC .
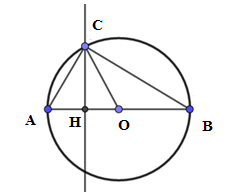
Diện tích hình tròn (O) là: S(O)=πR2
Ta có góc ^ACB là góc nội tiếp chắn nửa đường tròn ⇒^ACB=900⇒^BAC=900−^CBA=900−300=600.
Tam giác AOC có ^CAO=60∘ và OA=OC=R nên tam giác AOC đều cạnh bằng R .
Giả sử CH là đường cao của tam giác ABC , ta có:
CH=CO.sin600=√32.R⇒SABC=12CH.AB=12.√32R.2R=√32R2.
Diện tích hình giới hạn bởi đường tròn (O) và AC,BC là:
12S(O)−SABC=12πR2−√32R2=12(π−√3)R2=12(π−√3)(2√2)2=2π−2√3.
Cho đường tròn (O;R) và một điểm M sao cho OM=R√2. Từ M vẽ các tiếp tuyến MA,MB với đường tròn (A,B là các tiếp điểm ). Tính diện tích giới hạn bởi hai tiếp tuyến AM,MB và cung nhỏ AB.
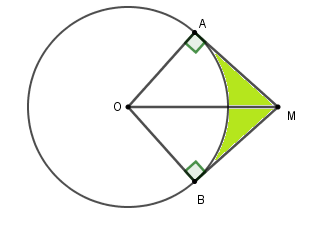
Xét ΔOAM có AM=√OM2−OA2=√2R2−R2=R⇒SOAM=OA.AM2=R22
Mà ΔOAM=ΔOBM(c−c−c)⇒SOAMB=2SOAM=R2
Xét ΔOAM có cos^AOM=OAOM=1√2⇒^AOM=45∘⇒^AOB=2.45∘=90∘
Diện tích quạt tròn SquạtAOB=πR2.90360=πR24
Diện tích phần giới hạn bởi hai tiếp tuyến AM,MB và cung nhỏ AB là
S=SOAMB−SquạtAOB=R2−πR24=(4−π)R24
Một hình quạt có chu vi bằng 34(cm) và diện tích bằng 66(cm2). Bán kính của hình quạt bằng?
Ta có {lR2=66l+2R=34⇔{lR=132l+2R=34⇔{l.2R=264l+2R=34⇔{2R=12l=22⇔{R=6l=22 .
Vậy R=6(cm)
Cho tam giác đều ABC nội tiếp đường tròn (O). Độ dài của các cung AB,BC,CA đều bằng 6π. Diện tích của tam giác đều ABC là:
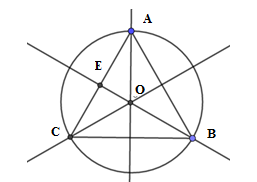
Gọi R là bán kính của đường tròn (O). Độ dài của các cung AB,BC,CA đều bằng 6π nên ta có C=2πR=6π+6π+6π=18π, suy ra R=9 hay OA=OB=OC=9
Ta cũng có ^AOB=^BOC=^COA=1200 suy ra ΔAOB=ΔAOC=ΔBOC suy ra SΔAOB=SΔAOC=SΔBOC=13SΔABC
Xét tam giác AOC có: {^OAC=^OCA=300^COA=1200
Kẻ đường caoOE , ta có đồng thời là đường trung tuyến, phân giác của góc ^COA . Ta có ^AOE=^COE=12^AOC
Xét tam giác COE có: {^ECO=300^CEO=900⇒OE=12CO=R2
Áp dụng định lý Pytago ta có: CE=√OC2−OE2=√R2−(R2)2=√32R
Vậy SCOE=12OE.CE=12.R2.√3R2=√3R28
Suy ra SCOA=2SCOE=√3R24 và SABC=3SCOA=3√3R24=3√3.924=243√34
Cho A,B,C,D là 4 đỉnh của hình vuông có cạnh là 2cm. Tính diện tích của hình hoa 4 cánh giới hạn bởi các đường tròn có bán kính bằng a, tâm là các đỉnh của hình vuông.
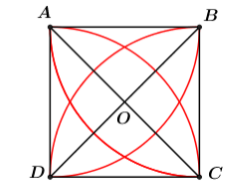
Ta có diện tích của hình hoa cần tính bằng 4 lần diện tích của hình viên phân AC: S=4SviênphânAC.
Hình viên phân AC bằng SquạtADC−SΔADC
Quạt tròn ADC có bán kính DA=DC=3cm và số đo cung 90∘
Có: SviênphânAC=SquạtADC−SΔADC=πR2.9003600−12R2=(π4−12)R2=π−24.22=π−2⇒S=4SviênphânAC=4.(π−2)=4π−8.
Một hình tròn có diện tích S=144π(cm2) . Bán kính của hình tròn đó là:
Diện tích S=πR2=144π⇔R2=144⇔R=12(cm).
Diện tích hình tròn bán kính R=10cm là
Diện tích S=πR2=π.102=100π(cm2).
Cho đường tròn (O,10cm), đường kính AB.. Điểm M∈(O) sao cho ^BAM=450. Tính diện tích hình quạt AOM .
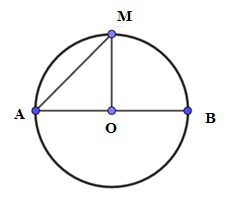
Xét đường tròn (O) có:
{OA=OM^MAO=450⇒ΔAOM là tam giác vuông cân.
⇒^MOA=900.
Vậy diện tích hình quạt AOM là S=πR2n360=π.102.90360=25π(cm2)
Cho đường tròn (O) đường kính AB= 4√3 cm .
Điểm C∈(O) sao cho ^ABC=300. Tính diện tích hình viên phânAC . (Hình viên phân là phần hình tròn giới hạn bởi một cung tròn và dây căng cung ấy).
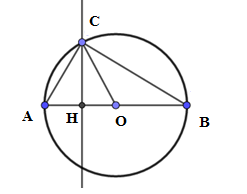
Xét đường tròn (O) có:
^ABC và ^AOC là góc nội tiếp và góc ở tâm cùng chắn cungAC ⇒^AOC=2.^ABC=2.300=600⇒SqAOC=πR2.60360=πR26
Xét ΔAOC có ^AOC=60∘ và OA=OC=R nên tam giác AOC đều cạnh bằng R .
Gọi CH là đường cao của tam giác AOC , ta có:
CH=CO.sin600=√32.R⇒SAOC=12CH.OA=12.√32.R.R=√34.R2.
Diện tích hình viên phân AC là:
SqAOC−SAOC=πR26−√34.R2=(π6−√34).R2
=(2π−3√312).(2√3)2
=2π−3√3cm2.
Cho hình vuông có cạnh là 5cm nội tiếp đường tròn (O). Hãy tính diện tích hình tròn (O).
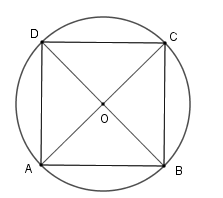
Gọi hình vuông ABCD nội tiếp đường tròn (O) khi đó OA=OB=OC=OD=R⇒O là giao điểm của AC và BD ⇒R=AC2.
Xét tam giác vuông ABC ta có AC2=AB2+BC2=52+52=50⇒AC=5√2 ⇒R=5√22
Diện tích hình tròn (O) là S=πR2=25π2(cm2).
Cho đường tròn (O) đường kính AB=2√2cm. Điểm C∈(O) sao cho ^ABC=300. Tính diện tích hình giới hạn bởi đường tròn (O) và AC,BC .
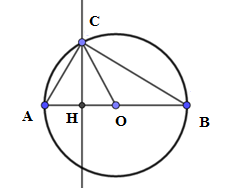
Diện tích hình tròn (O) là: S(O)=πR2
Ta có góc ^ACB là góc nội tiếp chắn nửa đường tròn ⇒^ACB=900⇒^BAC=900−^CBA=900−300=600.
Tam giác AOC có ^CAO=60∘ và OA=OC=R nên tam giác AOC đều cạnh bằng R .
Giả sử CH là đường cao của tam giác ABC , ta có:
CH=CO.sin600=√32.R⇒SABC=12CH.AB
=12.√32R.2R
=√32R2.
Diện tích hình giới hạn bởi đường tròn (O) và AC,BC là:
12S(O)−SABC=12πR2−√32R2=12(π−√3)R2=12(π−√3)(√2)2=π−√3.
Một hình quạt có chu vi bằng 28(cm) và diện tích bằng 49(cm2). Bán kính của hình quạt bằng?
Ta có {lR2=49l+2R=28⇔{lR=98l+2R=28⇔{l.2R=196l+2R=28⇔{2R=14l=14⇔{R=7l=14 .
Vậy R=7(cm)
Cho đường tròn (O;R) và một điểm M sao cho OM=2R. Từ M vẽ các tiếp tuyến MA,MB với đường tròn (A,B là các tiếp điểm ). Tính diện tích giới hạn bởi hai tiếp tuyến AM,MB và cung nhỏ AB.
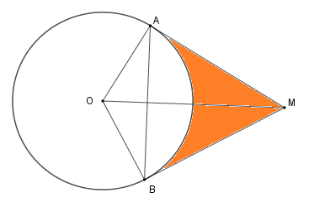
Xét ΔOAM có AM=√OM2−OA2=R√3⇒SOAM=OA.AB2=R2√32
Mà ΔOAM=ΔOBM(c−c−c)⇒SOAMB=2SOAM=√3R2
Xét ΔOAM có cos^AOM=OAOM=12
⇒^AOM=60∘⇒^AOB=120∘
Diện tích quạt tròn SqAB=πR2.120360=πR23
Diện tích giới hạn bởi hai tiếp tuyến AM,MB và cung nhỏ AB là
S=SOAMB−SqAB=√3R2−πR23=R2(√3−π3).
Cho tam giác đều ABC nội tiếp đường tròn (O). Độ dài của các cung AB,BC,CA đều bằng 4π. Diện tích của tam giác đều ABC là:
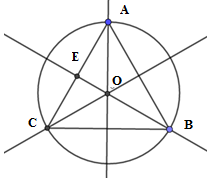
Gọi R là bán kính của đường tròn (O). Độ dài của các cung AB,BC,CA đều bằng 4π nên ta có C=2πR=4π+4π+4π=12π, suy ra R=6 hay OA=OB=OC=6
Ta cũng có ^AOB=^BOC=^COA=1200 suy ra ΔAOB=ΔAOC=ΔBOC=13ΔABC
Xét tam giác AOC có: {^OAC=^OCA=300^COA=1200
Kẻ đường caoOE , ta có đồng thời là đường trung tuyến, phân giác của góc ^COA . Ta có ^AOE=^COE=12^AOC
Xét tam giác COE có: {^ECO=300^CEO=900⇒OE=12CO=R2
Áp dụng định lý Pytago ta có: CE=√OC2−OE2=√R2−(R2)2=√32R
Vậy SCOE=12OE.CE=12.R2.√3R2=√3R28
Suy ra SCOA=2SCOE=√3R24 và SABC=3SCOA=3√3R24=3√3R24=27√3 cm2.
Cho A,B,C,D là 4 đỉnh của hình vuông có cạnh là a. Tính diện tích của hình hoa 4 cánh giới hạn bởi các đường tròn có bán kính bằng a, tâm là các đỉnh của hình vuông.
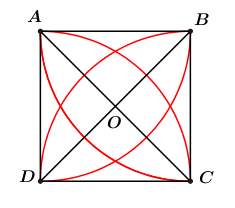
Ta có diện tích của hình hoa cần tình băng 4 lần diện tích của hình viên phânAC: S=4SvpAC.
Có: SvpAC=ScungAC−SADC=πR2.9003600−12R2=(π4−12)R2=π−24a2 ⇒S=4SvpAC=4.π−24a2=(π−2)a2.

